Question

In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find the number of people who read exactly one newspaper.

Answer 1

To solve the question, the have to calculate the number of people who read only newspaper H, only newspaper T and only newspaper I, by using the given information and by using the concept which states, the number of people who read only a certain newspaper is equal to the difference of the number of people who read that certain newspaper and the number of people who read other newspapers along with this certain newspaper. Thus, we can calculate the number of people who read only one newspaper, which is equal to the sum of the number of people who read only newspaper H, only newspaper T and only newspaper I.

Complete step-by-step answer :

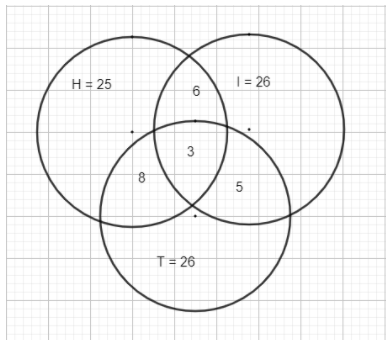
From the above Venn diagram, we get the information,
Total number of people participated in the survey = 60
Number of people who read newspaper H = 25
Number of people who read newspaper T = 26
Number of people who read newspaper I = 26
Number of people who read newspapers H and I = 9
Number of people who read newspapers H and T = 11
Number of people who read newspapers T and I = 8
Number of people who read all three newspapers = 3
We know that the number of people who read only a certain newspaper = The number of people who read that certain newspaper - The number of people who read other newspapers along with this certain newspaper + The number of people who read all the three newspapers.
By applying the above formula, we get
Number of people who read newspaper H only = Number of people who read newspaper H - Number of people who read newspapers H and I - Number of people who read newspapers H and T + Number of people who read all three newspapers
= 25 - 9 - 11 + 3
= 8
Number of people who read newspaper T only = Number of people who read newspaper T - Number of people who read newspapers H and T - Number of people who read newspapers T and I + Number of people who read all three newspapers
= 26 - 11 - 8 + 3
= 10
Number of people who read newspaper I only = Number of people who read newspaper I - Number of people who read newspapers H and I - Number of people who read newspapers T and I + Number of people who read all three newspapers
= 26 - 9 - 8 + 3
= 12
We know that the number of people who read only one newspaper is equal to sum of the number of people who read only newspaper H, only newspaper T and only newspaper I
Thus, we get
Number of people who read only one newspaper = 8 + 10 + 12 = 30

Note :The possibility of mistake can be, not able to analyse the given information to arrive at the solution since the question contains a large amount of data. The alternative way to solve the question is by using the direct formula $n(H\cup T\cup I)=n(H)+n(T)+n(I)-n(H\cap I)-n(H\cap T)-n(T\cap I)+n(H\cap T\cap I)$ where $n(H),n(T),n(I),n(H\cap I),n(H\cap T),n(T\cap I),n(H\cap T\cap I)$ represent the number of people who read newspaper H, the number of people who read newspaper T, the number of people who read newspaper I, the number of people who read newspapers H and I, the number of people who read newspapers H and T, the number of people who read newspapers T and I , the number of people who read all three newspapers and the number of people who read only one newspaper, respectively. Thus, by substituting the values in the above formula we can calculate the required answer.