Question

In a survey of 100 students, the number of students studying the various languages were found to be: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find how many students were studying Hindi?

Answer 1

In this question, we first need to draw the Venn-diagram and then find the unknown values from the given conditions. Then to find the students who study Hindi we need to find all the people who study only Hindi, Hindi and Sanskrit, Hindi and English and all the three and add them.

Complete step by step solution:
Let us first draw the Venn-diagram

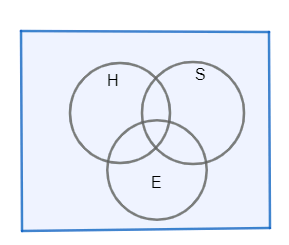
Let E, H, S be the students who are studying English, Hindi and Sanskrit respectively.
Now, from the given conditions and values in the question we get,

& n\left( U \right)=100 \\\ & n\left( E \right)=26 \\\ & n\left( S \right)=48 \\\ & n\left( E\cap S \right)=8 \\\ & n\left( S\cap H \right)=8 \\\ \end{aligned}$$ In the question given that the number of students that study Hindi but not English are 23. As we already know that the number of students that study both Hindi and Sanskrit are 8 and only English is 18. Now, by using the Venn-diagram we can get that $$n\left( E\cap S\cap H \right)=8-\left( 23-18 \right)$$ $$\therefore n\left( E\cap S\cap H \right)=3$$ In the question also given that the number of students who study no language are 24. Now, we can find the students studying only Sanskrit as $$\Rightarrow n\left( s \right)=n\left( S \right)-n\left( S\cap H \right)-n\left( E\cap S \right)+n\left( E\cap S\cap H \right)$$ Now, on substituting the respective values from the Venn-diagram we get, $$\begin{aligned} & \Rightarrow n\left( s \right)=48-8-8+3 \\\ & \therefore n\left( s \right)=35 \\\ \end{aligned}$$ Now, let us find the number of students who study only Hindi which can be given by $$\Rightarrow n\left( h \right)=n\left( U \right)-\left( n\left( E \right)+n\left( s \right)+n\left( S\cap H \right)-n\left( E\cap S\cap H \right) \right)-24$$ Now, on substituting the respective values in the above equation we get, $$\begin{aligned} & \Rightarrow n\left( h \right)=100-\left( 26+35+8-3 \right)-24 \\\ & \Rightarrow n\left( h \right)=100-66-24 \\\ & \therefore n\left( h \right)=10 \\\ \end{aligned}$$ Total number of students who study Hindi is given by $$\Rightarrow n\left( h \right)+3+5$$ Now, on substituting the value we get, $$\begin{aligned} & \Rightarrow 10+8 \\\ & \therefore 18 \\\ \end{aligned}$$ **Hence, the number of students who study Hindi are 18.** **Note:** Instead of finding the number of students who study only Hindi and then adding the students who study other languages also we can directly find it by subtracting the students who does not study anything and students who study only Sanskrit, only English and students who study English and Sanskrit then add the students who study all three from the total number students also give the same result. It is important to draw the Venn-diagram and calculate a particular number of students accordingly because neglecting any of the terms changes the result completely.