Question
Question: In a survey of 100 people it was found that 28 read magazine A, 30 read magazine B, 42 read magazine...
In a survey of 100 people it was found that 28 read magazine A, 30 read magazine B, 42 read magazine C, 8 read magazine A and B, 10 read magazine A and C, 5 read magazine B and C and 3 read all the three magazines. Find:
A. How many read none of the three magazines?
B. How many read magazine C only?
Solution
Hint: In order to solve this question, we will draw a Venn diagram to get the correct answer for both the options because it will give us a proper visualisation. We have to also be very focussed and careful while solving. In the Venn diagram, we will give each set a different name and then we will find the required value.
Complete step-by-step answer:
In this question, we are asked to find the number of persons who do not read any magazine and the number of persons who read only magazine C, when a few conditions are given. Let us consider the Venn diagram below.
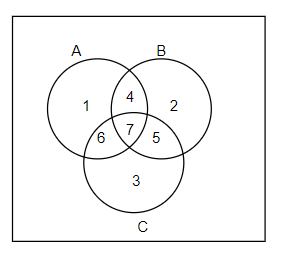
As we can see in the Venn diagram, we have considered the people who read magazine A only as 1, magazine B only as 2, magazine C only as 3, magazine A and B, but not C as 4, magazine B and C, but not A as 5, magazine C and A, but not B as 6 and all the magazines A, B and C as 7. Now we have been given that, 28 people read magazine A, so we can write it as,
n (1) + n (4) + n (6) + n (7) = 28 ……… (i)
And, 30 people read magazine B, so we get,
n (2) + n (4) + n (5) + n (7) = 30 ……… (ii)
Similarly, 42 people read magazine C, so,
n (3) + n (5) + n (6) + n (7) = 42 ……… (iii)
8 people read magazine A and B, so,
n (4) + n (7) = 8 ……… (iv)
10 people read magazine A and C, so,
n (6) + n (7) = 10 ……… (v)
5 people read magazine B and C, so,
n (5) + n (7) = 5 ……… (vi)
3 people read all the three magazines, so we get,
n (7) = 3 ……… (vii)
Now we will put the value of n (7) from equation (vii) in equation (iv), (v) and (vi). So, we get,
n (4) + 3 = 8 ; n (6) + 3 = 10 ; n (5) + 3 = 5
Which implies that, n (4) = 5 ……… (viii) ; n (6) = 7 ……… (ix) ; n (5) = 2 ……… (x)
Now we will use the values of n (4), n (6) and n (7) in equation (i). So, we get,
n (1) + 5 + 7 + 3 = 28
n (1) = 13 ……… (xi)
Now, we will use the values of n (4), n (5) and n (7) in equation (ii). So, we get,
n (2) + 5 + 2 + 3 = 30
n (2) = 20 ……… (xii)
And we will now use the value of n (5), n (6) and n (7) in equation (iii). So, we get,
n (3) + 2 + 7 + 3 = 42
n (3) = 30 ……… (xiii)
Now that we have found out all the values, let us consider the options one by one.
A. Number of people who do not read any of the magazines.
We can calculate the same by subtracting the number of people who read at least one magazine from 100, which was the total number of people, so we get,
100 - [ n (1) + n (2) + n (3) + n (4) + n (5) + n (6) + n (7)]
Now we will put all the values and get,
100 - [13 + 20 + 30 + 5 + 2 + 7 + 3]
100 - 80 = 20
Hence, the number of people who do not read any magazine is 20.
B. Number of people who read only magazine C.
We can calculate it by finding the value of n (3), and from equation (xiii), we can say that n (3) = 30.
Hence, the number of people who read only magazine C is 30.
Note: We need to be highly focussed and careful while solving this question as the possibility of making calculation mistakes is very high. We can also solve part A of the question by using the formula of n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(A∩C)+n(A∩B∩C) . And after calculating the value of n(A∪B∪C), we can subtract it from 100 to get the desired result.
