Question

In a survey it was found that 21 people liked product A. 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked product B and C and 8 liked all three of them. Find how many liked product C only.

Answer 1

We first define the events. Then we mathematically express each and every case of the number of people liking an event. We try to form the Venn diagram using the number. Then we find the case which defines the event of people liking product C only. We place the values to find the solution of the problem.

Complete step by step answer:
We define the events of liking the products according to the product name.
So, A, B, C defines the event of liking the products A, B, C respectively.
We have been given a number of people liking different products. We represent them in a mathematical way.
21 people liked product A. 26 liked product B and 29 liked product C.
So, $n\left( A \right)=21,n\left( B \right)=26,n\left( C \right)=29$.
When someone likes two products then that means we are taking an intersection.
14 people liked products A and B, 12 people liked products C and A, 14 people liked product B and C.
So, $n\left( A\cap B \right)=14,n\left( B\cap C \right)=14,n\left( A\cap C \right)=12$.
8 liked all three of them which means $n\left( A\cap B\cap C \right)=8$.
We need to find a number of people who like product C only.
So, mathematically we are trying to find $n\left( {{A}^{c}}\cap {{B}^{c}}\cap C \right)$. Here ${{A}^{c}},{{B}^{c}}$ defines the complement event of A and B respectively. Now, we try to form the Venn diagram.

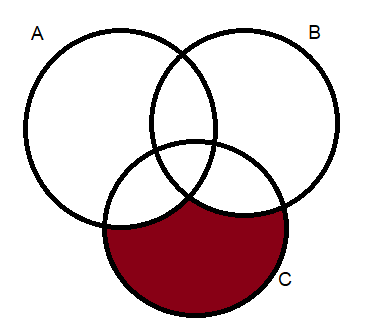
Now we know that
$n\left( {{A}^{c}}\cap {{B}^{c}}\cap C \right)=n\left( C \right)-\left[ n\left( B\cap C \right)+n\left( A\cap C \right) \right]+n\left( A\cap B\cap C \right)$.
We take the whole C event. We eliminate two events where people liked A and B with C. But in that case the event where people liked all three cases is being eliminated twice. So, we add that one.
Now we place values to get
$\begin{aligned} & n\left( {{A}^{c}}\cap {{B}^{c}}\cap C \right)=n\left( C \right)-\left[ n\left( B\cap C \right)+n\left( A\cap C \right) \right]+n\left( A\cap B\cap C \right) \\\ & \Rightarrow n\left( {{A}^{c}}\cap {{B}^{c}}\cap C \right)=29-14-12+8=11 \\\ \end{aligned}$

So, the number of people who liked product C only is 11.

Note: We need to remember Venn diagram is only to visualise the problem in the form of diagram. We don’t need to consider the whole event and find its solution as it won’t be necessary to solve the problem .so, we always need to form the required event in the form of mathematical notion.