Question

In a square cut, the speed of cricket ball changes from $30m{s^{ - 1}}$ to $40m{s^{ - 1}}$ during the time of its contact $\Delta t = 0.01s$ with the bat. If the ball is deflected by the bat through an angle of $\theta = 90^\circ$ , find the magnitude of the average acceleration (in $\times {10^2}m{s^{ - 2}}$ ) of the ball during the square cut.

Answer 1

Although acceleration is nothing but change in velocity per unit time, here we can see that there will be a change in direction clearly along with the change in magnitude. So, we should be seeing the velocity as a vector quantity and not a scalar quantity.

Formulas used We will be using the formula $a = \dfrac{{{v_2} - {v_1}}}{{\Delta t}}$ where ${v_1}$ is the initial velocity, ${v_2}$ is the final velocity, and $\Delta t$ is the time taken to cause the change in velocity from ${v_1}$ to ${v_2}$ . Also we will be using the formula $\left| {\overrightarrow {\Delta v} } \right| = \sqrt {(v_1^2 + v_2^2 - 2{v_1}{v_2}\cos \theta )}$ where $\theta$ is the angle of deflection between the final and initial velocities.

Complete Answer:
We know that the acceleration of a body is the rate of change of velocity of that body, but we also know that the velocity is a vector quantity and not a scalar quantity. So, the velocity as a vector has both magnitude and direction.
Here the velocity vector approaches the surfaces of the bat and then leaves the bat at a different magnitude of velocity and an angle of deflection $\theta = 90^\circ$ .

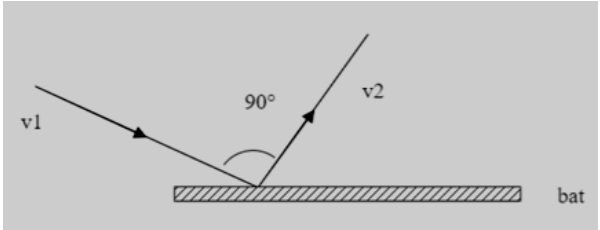
So, the resultant of this velocity vector $\overrightarrow v$ will be $\left| {\overrightarrow {\Delta v} } \right| = \sqrt {(v_1^2 + v_2^2 - 2{v_1}{v_2}\cos \theta )}$ . Substituting the values of ${v_1} = 30m/s$ , ${v_2} = 40m/s$ and $\theta = 90^\circ$ we get. $\left| {\overrightarrow {\Delta v} } \right| = \sqrt {({{(30)}^2} + {{(40)}^2} - 2(30)(40)\cos 90^\circ )}$
We know $\cos 90^\circ = 1$ so, $\left| {\overrightarrow {\Delta v} } \right| = \sqrt {(900 + 1600 - 2(30)(40)(0))}$
$\Rightarrow \left| {\overrightarrow {\Delta v} } \right| = \sqrt {(2500)} = 50$
The resultant velocity will be $\left| {\overrightarrow {\Delta v} } \right| = 50m/s$ . Now using $a = \dfrac{{\left| {\overrightarrow {\Delta v} } \right|}}{{\Delta t}}$ we could find the value of $a$ to be $\Rightarrow a = \dfrac{{50}}{{0.01}} = 5000m/{s^2}$ (since $\Delta t = 0.01s$ )
Thus, the average acceleration of the ball during the square cut is $50 \times {10^2}m/{s^2}$ .

Note:
We can consider the velocity to be scalar in cases where the body does not show a change in direction or does not experience the deflection from its original path. In other situations, we are supposed to consider the velocity as a vector to obtain the exact answer by finding the resultant of the vectors involved.