Question

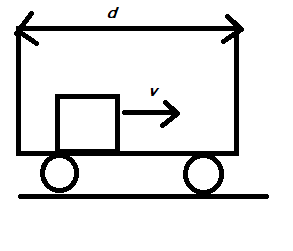
In a smooth stationary cart of length $d$, a small block is projected along its length with velocity $v$ towards front. Coefficient of restitution for each collision is $e$. The cart rests on a smooth ground and can move freely. The time taken by block to come to rest wrt cart is

$\begin{aligned} & A.\dfrac{ed}{(l-e)v} \\\ & B.\dfrac{ed}{(l+e)v} \\\ & C.\dfrac{d}{e} \\\ & D.\infty \\\ \end{aligned}$

Answer 1

To find the time when the block comes to rest, let use the given velocity and the distance. Since the velocity of the block after the collision is unknown. Let us use the given coefficient of restitution, to find the velocity after each collision.

Formula used:
$e=\dfrac{vel\; after\; collision}{vel\; before\;collision}$ and $speed=\dfrac{distance}{time}$

Complete answer:
Let us assume that there is no external force acting on the block and is confined to the walls of the cart Let us also assume that the block comes to rest after $n$ collisions with the walls of the container. Since the block is confined to the cart, then the maximum distance covered by the block is $d$.
Given that the velocity of the block is $v$ and the coefficient of restitution for each collision is $e$. Where the coefficient of restitution is the ratio is velocity of the block after collision to velocity of the block before collision.
i.e. $e=\dfrac{vel\; after\; collision}{vel\; before\;collision}$
Then, we can find the velocity after $1^{st}$ collision as $ve$
Similarly, for the velocity after $n$ collisions is $ve^{n}$
Since we know that, $speed=\dfrac{distance}{time}$
Then, the time taken for $n$ collisions is given by $t= \dfrac{d}{v}+\dfrac{d}{ve}+\dfrac{d}{ve^{2}}+..+\dfrac{d}{ve^{n}}$
Or, we get $t=\dfrac{d}{v}\left[1+\dfrac{1}{e}+\dfrac{1}{e^{2}}+..\dfrac{1}{e^{n}}\right]$
Since the series $\dfrac{1}{e}$ is converging, we get,
$t=\dfrac{d}{v}[1+\infty]$
We know that any number added to $\infty$ results in $\infty$.
Hence, we get $t=\infty$

So, the correct answer is “Option D”.

Note:
Here it is assumed that the block collides with the walls of the cart at a velocity $v$, then it rebounds with a velocity $ve$. Then, the new velocity of the block is $ve$, again the block collides with the other wall of the cart, then it rebounds with $ve^{2}$. Each time it covers a distance $d$.