Question

In a single slit experiment, the width of the slit is reduced. Then, the linear width of the principal maxima ________.

A.Increases but becomes less bright
B.Decreases but becomes more bright
C.Increases but becomes more bright
D.Decreases but becomes less bright

Answer 1

Hint: Width of the principal maxima, also called a central bright fringe, depends upon the wavelength of incident light, width of slit and distance between slit and screen.
Formula used:

$w=\dfrac{\lambda D}{d}$

Complete step by step answer:
Single slit diffraction is observed when light passes through a single slit of width $w$which is of the order of wavelength of incident light. The diffraction pattern is observed at some distance (say$d$) from the slit. Also, the intensity of different fringes observed on the screen is a function of angle between successive phasors.

Width of Central or Principal Maxima is the distance between the first order minima from the centre of screen on both the sides of centre.

Expression for width of Principal maxima:

$w=\dfrac{\lambda D}{d}$
Where $w$= width of central or principal maxima
$\lambda$= wavelength of the incident light
$d$= width of the slit
$D$= distance between the slit and the screen

If we decrease the width of the slit $d$, keeping all other parameters the same, then width of principal maxima will be increased as width of principal maxima is inversely proportional to the width of slit.

The intensity of central maxima is denoted by ${{I}_{o}}$. In a single slit diffraction experiment, central or principal maxima is the brightest fringe observed having maximum intensity equal to ${{I}_{o}}$. As we move away from the centre, intensity at corresponding maximas decreases as compared to the intensity at central maxima.

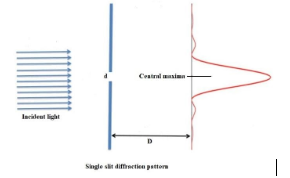
In a single slit diffraction pattern, the resultant amplitude can be obtained by dividing the slit width into a large number of equal segments. For each segment, the amplitude is taken proportionally equal and a constant phase difference is also taken between the adjacent segments. So, the amplitude is directly proportional to the width of slit and intensity will be proportional to the square of the slit width.

If we decrease the width of slit, then resultant amplitude of wave would also be decreased resulting in the decrease in intensity at the central maxima and we will get a less bright principal maxima.

Decreasing slit width increases the linear width of principal maxima and decreases the intensity at principal maxima.

Hence, the correct option is A.

Note:
Diffraction is evident only when the sources are small enough that are relatively the order of the wavelength of the light. Students should not get confused between the Linear width and Angular width of a fringe. In the above question, we worked on Linear width only. Angular fringe width for small angle,$\theta =\dfrac{\lambda }{d}$ .