Solveeit Logo
Login

Question

Question: In a series resonant circuit, having \(L,C\text{ and }R\) as its elements, the resonant current will...

In a series resonant circuit, having L,C and RL,C\text{ and }R as its elements, the resonant current will be found to be as ii. What will be the power dissipated in the circuit at resonance?
A.i2lω B.i2R C.zero D.i2Cω \begin{aligned} & A.{{i}^{2}}l\omega \\\ & B.{{i}^{2}}R \\\ & C.zero \\\ & D.{{i}^{2}}C\omega \\\ \end{aligned}

Explanation

Solution

The effective resistance of the circuit can be found by taking the square root of the sum of the square of the resistance and the square of the difference between the product of inductance and resonant frequency and the reciprocal of the product of the capacitance and the resonant frequency. Find the effective power by substituting the resonance frequency equation. Power dissipated will be a product of the square of the current and the effective resistance. This will help you in answering this question.

Complete answer:

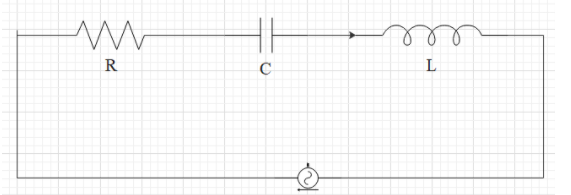
it has been already mentioned in the question that the series resonant circuit is having L,C and RL,C\text{ and }R as its elements. The resonant current in the circuit has been found to be as ii. The effective resistance of the circuit can be found by taking the square root of the sum of the square of the resistance and the square of the difference between the product of inductance and resonant frequency and the reciprocal of the product of the capacitance and the resonant frequency. This can be written as,
X=R2+(Lω−1Cω)2X=\sqrt{{{R}^{2}}+{{\left( L\omega -\dfrac{1}{C\omega } \right)}^{2}}}
At the resonance the angular frequency can be written as,
ω=1LC\omega =\dfrac{1}{\sqrt{LC}}
Therefore the effective resistance will become,
X=RX=R
The power dissipated will be a product of the square of the current and the resistance.
P=i2RP={{i}^{2}}R
Therefore the correct answer for the power dissipated has been obtained.

This has been mentioned as option B.

Note:
The primary difference between a capacitor and an inductor is that a capacitor will prevent a variation in voltage. But an inductor will prevent a variation in the current. The inductor is used to store energy in the form of a magnetic field, and the capacitor is used to store energy in the form of an electric field.