Question

In a series LR circuit, the voltage drop across the inductor is $8{\text{ }}volt$ and across the resistor is $6{\text{ }}volt$ . The voltage applied and the power factor of the circuit respectively are
A. $14V,0.8$
B. $10V,0.8$
C. $10V,0.6$
D. $14V,0.6$

Answer 1

By using the given values first we have to calculate all the parameters that are given in the options. This will give us a fair idea of which one will be the correct option from the given option. The formula of the Power factor and resultant voltage of the LCR circuit can be used to calculate the required answer.

Formula used:
The net voltage ${V_{net}} = \sqrt {{V_r}^2 + {V_i}^2}$
The power factor= $\dfrac{{{V_r}}}{{{V_{net}}}}$
Where, ${V_r}$- The voltage drop across the resistor, ${V_i}$- The voltage drop across the inductor

Complete step by step answer:
The circuit is given by,

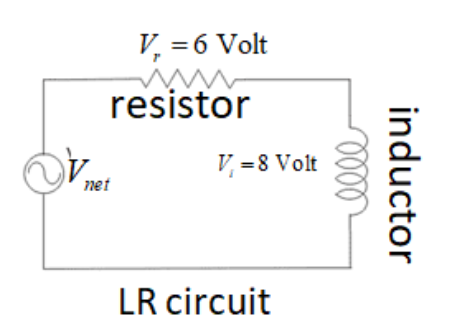
The phase vectors of a resistor and an inductor make an angle of ${90^ \circ }$ each other. Hence, the net voltage will be obtained by taking the vector sum:
${V_{net}} = \sqrt {{V_r}^2 + {V_i}^2}$
$\Rightarrow {V_{net}} = \sqrt {{6^2} + {8^2}} = 10V$

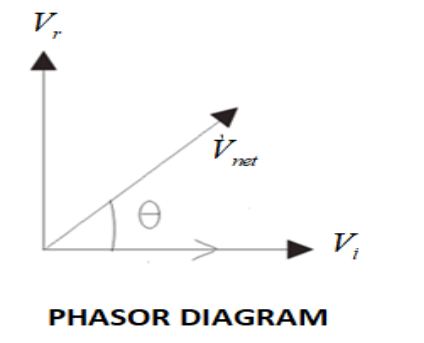
Now let us calculate the power factor, the power factor is defined as the ratio of true power to apparent power will be given by $\dfrac{{{V_r}}}{{{V_{net}}}}$. Since the current flow through the inductor and resistor is the same.

\Rightarrow \text{Power factor} = \dfrac{6}{{10}} \\\ \therefore \text{Power factor} = 0.6$$ The voltage applied and the power factor of the circuit respectively are $$10V$$ and $$0.6$$. **Hence, option C is correct.** **Note:** Remember that if $${V_c} > {V_i}$$ then current will always lead to the voltage.Always remember that the power factor is defined as the ratio of the real power that is used to do work and the apparent power that is supplied to the circuit. The power factor can get values in the range from $$0$$ to $$1$$. When all the power is reactive power then the power with no real power (usually inductive load) the power factor is $$0$$.