Question

In a series LCR circuit $R=4\Omega$, ${{X}_{L}}=5\Omega$ and ${{X}_{C}}=8\Omega$, the current
A. leads the voltage by ${{\tan }^{-1}}\left( \dfrac{3}{4} \right)$
B. leads the voltage by ${{\tan }^{-1}}\left( \dfrac{5}{8} \right)$
C. leads the voltage by ${{\tan }^{-1}}\left( \dfrac{3}{5} \right)$
D. leads the voltage by ${{\tan }^{-1}}\left( \dfrac{5}{9} \right)$

Answer 1

As a first step, you could recall the expression for phase angle in terms of inductive reactance, capacitive reactance and resistance as these are the given quantities in the question. Or else you could derive the same from the phasor diagram or the impedance diagram. Also, remember that $\phi$ gives the angle by which current leads the voltage. Now, simple substitution will give you the answer.
Formula used:
Expression for phase angle,
$\tan \phi =\dfrac{{{X}_{C}}-{{X}_{L}}}{R}$

Complete answer:

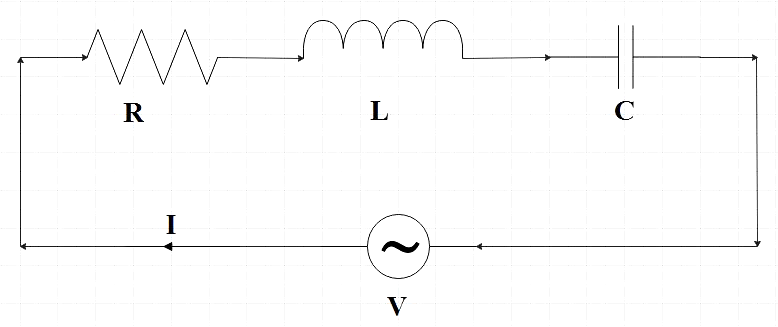
In the figure, we have a series LCR circuit. Since the connection is made in series, the ac current is always same in each element and is given by,
$I={{I}_{0}}\sin \left( \omega t+\phi \right)$
Where, ‘$\phi$’ is the phase difference between the current in the circuit and the voltage across the source. The phasor diagram with ${{V}_{L}}$, ${{V}_{C}}$, ${{V}_{R}}$ and $I$ is given by,

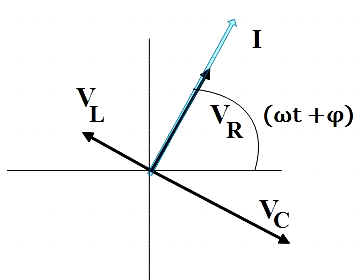
The amplitude of - ${{V}_{L}}$, ${{V}_{C}}$ and ${{V}_{R}}$ is given respectively by,
${{V}_{0L}}={{I}_{0}}{{X}_{L}}$ ……………………. (1)
${{V}_{0C}}={{I}_{0}}{{X}_{C}}$ …………………. (2)
${{V}_{0R}}={{I}_{0}}R$……………………. (3)
Where, ${{X}_{L}}$ and ${{X}_{C}}$ are the reactance of the inductor and capacitor respectively and R is the resistance of the resistor. All three can be defined as the opposition offered by the respective elements to the flow of current in the circuit.

From the figure we see that the phasor $I$ is always parallel to phasor ${{V}_{R}}$, so the phase angle $\phi$ can be said as the angle between ${{V}_{R}}$ and $V$. Tangent of the phase angle is given by,
$\tan \phi =\dfrac{{{V}_{0C}}-{{V}_{0L}}}{{{V}_{0R}}}$
Substituting (1), (2), (3), we get,
$\Rightarrow \tan \phi =\dfrac{{{I}_{0}}\left( {{X}_{C}}-{{X}_{L}} \right)}{{{I}_{0}}R}$
$\Rightarrow \tan \phi =\dfrac{{{X}_{C}}-{{X}_{L}}}{R}$ ………………………….. (4)
Given values in the question are:
$R=4\Omega$
${{X}_{C}}=8\Omega$
${{X}_{L}}=5\Omega$
Substituting these values in equation (4), we get,
$\Rightarrow \tan \phi =\dfrac{8-5}{4}$
$\Rightarrow \tan \phi =\dfrac{3}{4}$
$\Rightarrow \phi ={{\tan }^{-1}}\left( \dfrac{3}{4} \right)$
From the phasor diagram we know that the current leads voltage by a phase difference of$\phi$. Therefore, the current leads the voltage by ${{\tan }^{-1}}\left( \dfrac{3}{4} \right)$.

So, the correct answer is “Option A”.

Note:
You shouldn’t necessarily derive the tangent of the phase difference from the phasor diagram. We have done it here for better understanding of the concept. You could simply memorize the standard expression for $\phi$ and hence save time while solving numerical problems like this.