Question

In a series LCR AC circuit, the current is maximum when the impedance is equal to:
A. the reactance
B. the resistance
C. zero
D. twice the reactance
E. twice the resistance

Answer 1

The resistance is the property of the resistor to resist the flow of current through the circuit. The inductive reactance is the resistance offered by the inductor. The capacitive reactance is the resistance offered by the capacitor. The current is the emf by the impedance.

Complete step-by-step solution:
The properties of the electrical components used to solve this problem are: The resistance is the property of the resistor to resist the flow of current through the circuit. The inductive reactance is the resistance offered by the inductor. The capacitive reactance is the resistance offered by the capacitor. In general, the overall capacitive reactance and the inductive reactance is simply called the reactance.
According to Ohm’s law, the current is voltage by the resistance. In the case of the AC circuit, the current is the emf by the impedance. Here, the impedance equals the root of the sum of the squares of resistance and the (difference/sum of the inductive and the capacitive reactance).
Consider the circuit diagram.

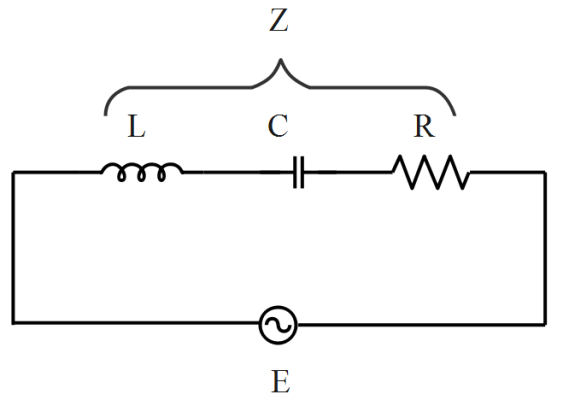
According to Ohm’s law, the relation between the current, voltage and impedance is,
$I=\dfrac{E}{Z}$
Where I is the current, E is the emf and Z is the total impedance.
The mathematical representation of the same is given as follows.
$I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}}$
When the inductive reactance equals the capacitive reactance, we get,

& I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{L}} \right)}^{2}}}} \\\ & \Rightarrow I=\dfrac{{{E}_{0}}}{\sqrt{{{R}^{2}}}} \\\ & \therefore I=\dfrac{{{E}_{0}}}{R} \\\ \end{aligned}$$ As the above equation has a smaller denominator value, thus, the maximum amount of current will flow. **$$\therefore $$ In a series LCR AC circuit, the current is maximum when the impedance is equal to the resistance, thus, option (B) is correct.** **Note:** In the case of a capacitor, voltage lags current by $$90{}^\circ $$. In the case of an inductor, voltage leads current by $$90{}^\circ $$. Therefore, the voltages on the inductor and capacitor are $$180{}^\circ $$out of phase with each other so they have to be subtracted.