Question

In a series $CR$ circuit shown in figure, the applied voltage is $10V$ and the voltage across the capacitor is found to be $8V$ . The voltage across $R$ , and the phase difference between the current and the applied voltage respectively be:

A. $6V,{\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$
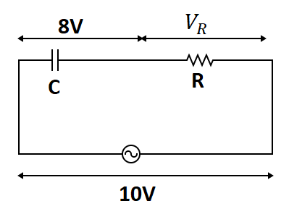
B. $3V,{\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$
C. $6V,{\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$
D. None of these

Answer 1

In this question we need to find the voltage across the resistor by using the capacitor voltage and the supply voltage and we also need to find the phase difference between the capacitor and the resistor by using the given data. The capacitor, inductor and resistor are the passive components where capacitor and inductor are the components which are used to store the energy, capacitor will store energy in the form of electrical energy whereas the inductor will store the energy in the form of magnetic field.

Formulas used:
$\to {V^2} = \sqrt {{V_R} + {{({V_L} - {V_c})}^2}}$
Where, ${V_R} =$ Voltage across the resistor, ${V_L} =$ Voltage across the inductor, ${V_C} =$Voltage across the capacitor and ${V_{}} =$ Source voltage.
$\tan \phi = \dfrac{{{V_c} - {V_L}}}{{{V_R}}}$
Where, $\phi =$ Phase difference

Complete step by step answer:
Given:- $V = 10V$, ${V_c} = 8V$, ${V_L} = 0$, ${V_R} = ?$ and $\phi = ?$.
We know that,
${V^2} = \sqrt {{V_R} + {{({V_L} - {V_c})}^2}}$
Here, ${V_L} = 0$
Therefore, ${V^2} = \sqrt {V_R^2 + {V_c}^2}$
On further simplification
${V_R} = \sqrt {{{\left( V \right)}^2} - {{\left( {{V_C}} \right)}^2}}$
On substituting the given data in above equation we get
${V_R} = \sqrt {{{\left( {10} \right)}^2} - {{\left( 8 \right)}^2}}$
Therefore, ${V_R} = 6V$
And, $\tan \phi = \dfrac{{{V_c} - {V_L}}}{{{V_R}}}$
On substituting the given data in above equation we get
$\tan \phi = \dfrac{8}{6} = \dfrac{4}{3}$
$\therefore \phi = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$

Hence, option A is correct.

Note: The capacitive reactance and inductive reactance is the resistance offered by the capacitor and inductor respectively. An alternating circuit can contain capacitor or inductor or both capacitor and inductor. The S.I unit for the capacitive reactance and inductive reactance is $\Omega$ . In the circuit containing the resistor only the current and voltage will have zero phase difference whereas in the circuit containing the capacitor only the current leads the voltage by ${90^0}$. In the circuit containing the inductor only the current lags the voltage by ${90^0}$.