Question

In a school, there are 40 teachers who teach mathematics or physics. Of these 24 teach mathematics and 8 teach both mathematics and physics. How many teachers teach only physics?
[a] 4
[b] 12
[c] 8
[d] 16

Answer 1

Assume that A be the set of the teachers teaching mathematics and B the set of the teachers teaching physics. Use the fact that $n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right)$. Put $n\left( A\bigcup B \right)=40,n\left( A \right)=24$ and $n\left( A\bigcap B \right)=8$. Hence find the value of n(B). Hence find the number of teachers teaching physics. Alternatively, solve using Venn-diagram.

Complete step by step answer:
Let A be the set of the teachers teaching mathematics and B be the set of the teachers teaching physics.
Hence, we have $A\bigcap B$ is the set of the teachers teaching both physics and mathematics and $A\bigcup B$ is the set of the teacher teaching physics or mathematics.
Since the number of teachers teaching mathematics or physics is 40, we have
$n\left( A\bigcup B \right)=40$
Since the number of teachers teaching mathematics is 24, we have n(A) = 24
Since the number of teachers teaching both mathematics and physics is 8, we have
$n\left( A\bigcap B \right)=8$
Now, we know that for any two countably finite sets A and B, we have
$n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right)$
Hence, we have
$\begin{aligned} & 40=24+n\left( B \right)-8 \\\ & \Rightarrow n\left( B \right)+16=40 \\\ \end{aligned}$
Subtracting 16 from both sides of the equation, we get
n(B) = 24.
Hence the number of teachers teaching physics is 24
Now, the number of teachers who teach only physics is equal to the number of teachers who teach both mathematics and physics subtracted from the number of teachers who teach physics = 24-8 = 16

So, the correct answer is “Option d”.

Note: Alternative Solution using Venn-diagrams

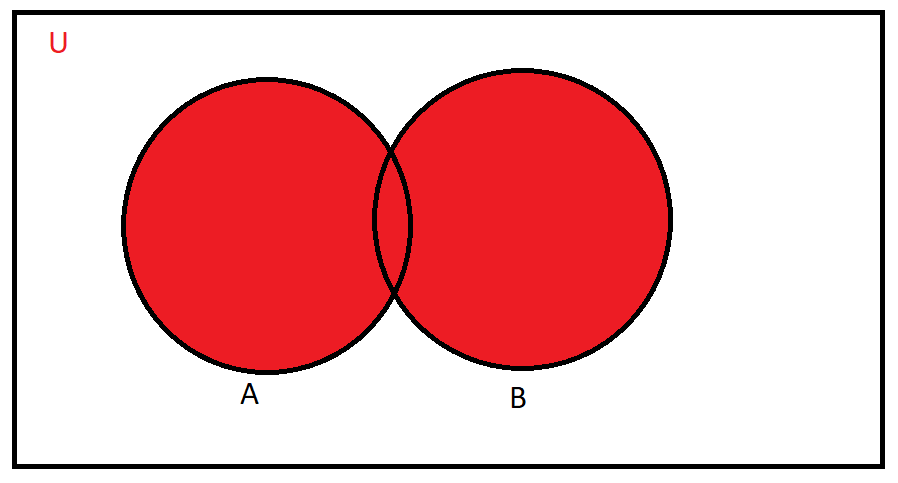
Number of teachers in red region = 40

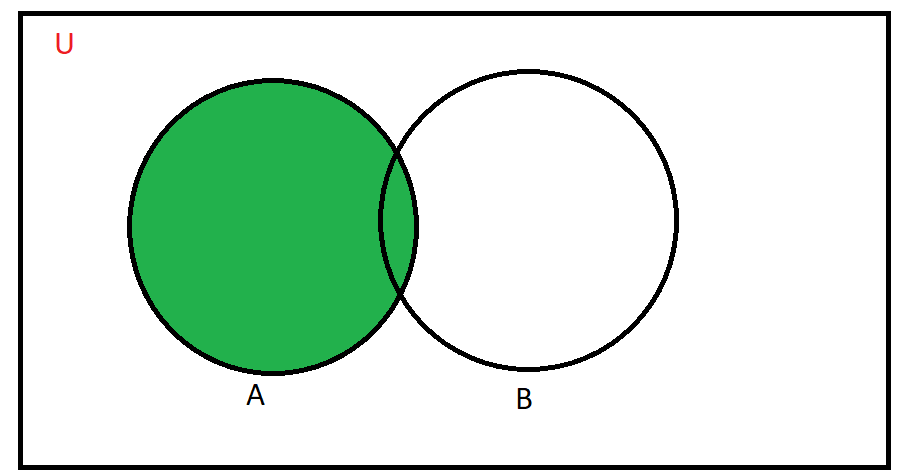
Number of teachers in green region = 24
Now because we need the number of teachers who teach Physics therefore we need to subtract the number of teachers who teach both Mathematics and physics, it is represented by the yellow region given below,

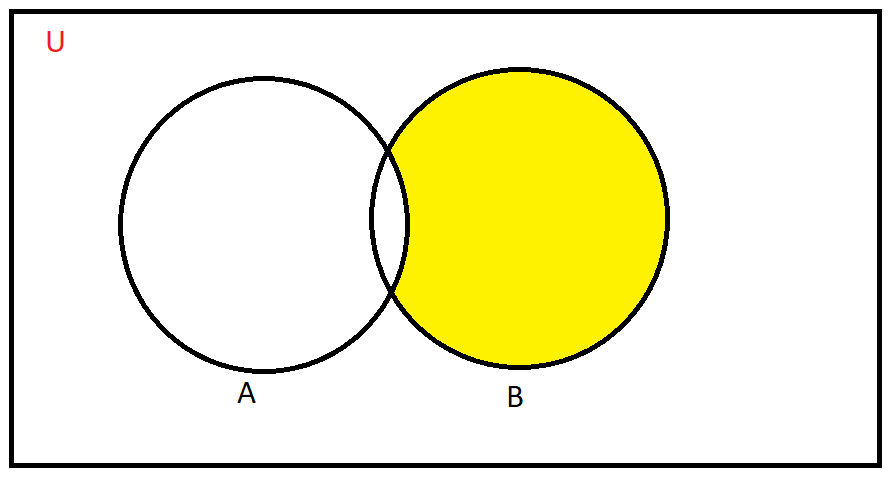
Hence the number of teachers in the yellow region = 40-16=24
Hence the number of teachers teaching only physics is 24, which is the same as obtained above.
Hence option [d] is correct.