Question
Question: In a scattering experiment, a particle of mass $2m$ collides with another particle of mass $m$, whic...
In a scattering experiment, a particle of mass 2m collides with another particle of mass m, which is initially at rest. Assuming the collision to be perfectly elastic, the maximum angular deviation θ of the heavier particle, as shown in the figure, in radians is:
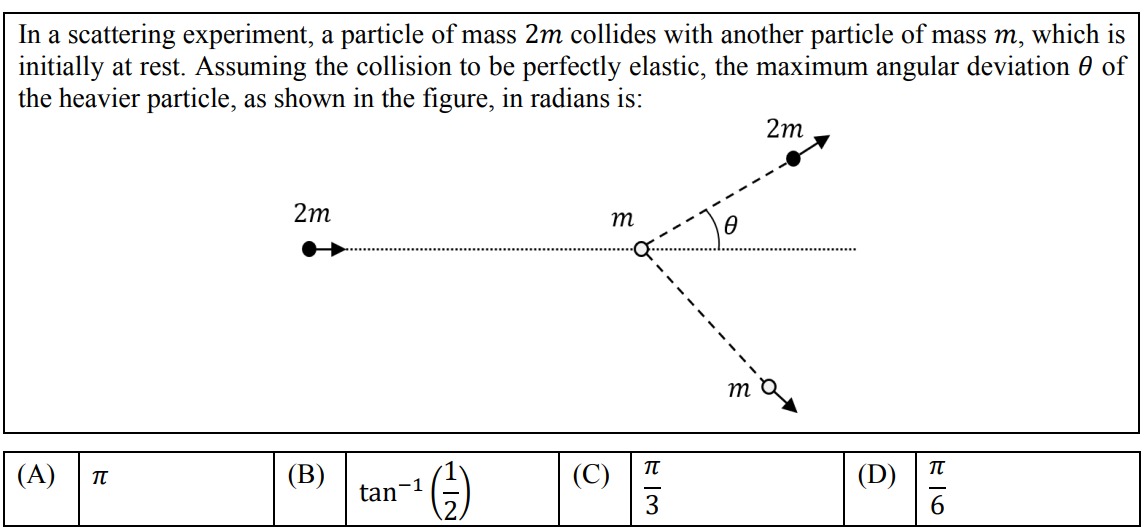
π
tan−1(21)
3π
6π
6π
Solution
The problem involves an elastic collision between two particles. To find the maximum angular deviation θ of the heavier particle, we can use the formula derived from conservation of momentum and kinetic energy.
Method 1: Using the center of mass frame
-
Velocity of the Center of Mass (VCM): VCM=m1+m2m1u1+m2u2=2m+m2mu1=32u1
-
Velocities in the Center of Mass (CM) Frame: u1′=u1−VCM=u1−32u1=31u1 u2′=u2−VCM=0−32u1=−32u1
-
Relating Lab Frame and CM Frame Velocities: v1=v1∗′+VCM v1x=VCM+v1∗′cosϕ=32u1+31u1cosϕ v1y=v1∗′sinϕ=31u1sinϕ
-
Scattering Angle of Incident Particle (θ1): tanθ1=v1xv1y=32u1+31u1cosϕ31u1sinϕ=2+cosϕsinϕ
-
Maximizing θ1: dϕd(tanθ1)=(2+cosϕ)22cosϕ+1=0⟹cosϕ=−21 sinϕ=±1−(−21)2=±23. tanθ1=2+(−21)23=2323=33=31 θ1=tan−1(31)=6π radians.
Method 2: Using the general formula for maximum scattering angle
θmax=sin−1(m1m2)=sin−1(2mm)=sin−1(21)=6π radians.
Therefore, the maximum angular deviation θ of the heavier particle is 6π radians.
