Question

In a right angled triangle, if one angle is ${45^ \circ }$ and the opposite side to it is $k$ times the hypotenuse, then the value of $k$ is
A. $1$
B. $\dfrac{1}{2}$
C. $\dfrac{1}{{\sqrt 2 }}$
D. $\sqrt 2$

Answer 1

Here given that there is a right angled triangle. To solve this problem we should know the most important properties of a triangle. First property is that in any triangle, the sum of the angles in a triangle should be equal. If any two angles in a triangle are equal then the two opposite sides of those angles are equal. If two sides are equal in a triangle then it is called an isosceles triangle.

Complete step by step answer:
Given that the triangle is a right angled triangle, and also given that one of its angles is ${45^ \circ }$.
Let the triangle be ABC.

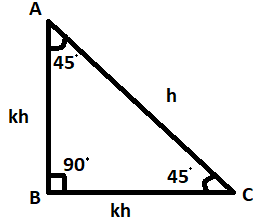
In a right angled triangle one angle is ${90^ \circ }$.
Let $\angle B = {90^ \circ }$ and let $\angle C = {45^ \circ }$, as given one of the angles is ${45^ \circ }$.
The sum of all the angles in a triangle should be equal to ${180^ \circ }$, which is given by:
$\Rightarrow \angle A + \angle B + \angle C = {180^ \circ }$
$\Rightarrow \angle A + {90^ \circ } + {45^ \circ } = {180^ \circ }$
$\therefore \angle A = {45^ \circ }$
Hence $\angle A = \angle C$
$\therefore \Delta ABC$is a right isosceles triangle.
Thus the two sides other than the hypotenuse should be equal, which is given by:
$\Rightarrow AB = BC$
Given that the side opposite to the angle ${45^ \circ }$ is $k$ times the hypotenuse, which is given by:
Let the length of hypotenuse $AC$ be $h$, and as the side opposite to the angle ${45^ \circ }$ is $k$ times the hypotenuse:
$\Rightarrow AC = h$
As $AB$ and $BC$ are the sides opposite to angles ${45^ \circ }$, the lengths of the sides is given by:
$\Rightarrow$ $AB = kh$
Hence $BC = kh$, as $AB = BC$
A right angled triangle satisfies the pythagoras theorem which is given by:
$\Rightarrow A{B^2} + B{C^2} = A{C^2}$
$\Rightarrow {(kh)^2} + {(kh)^2} = {h^2}$
$\Rightarrow 2{k^2}{h^2} = {h^2}$
Here ${h^2}$ gets cancelled on both sides.
$\Rightarrow 2{k^2} = 1$
$\Rightarrow {k^2} = \dfrac{1}{2}$
$\Rightarrow k = \dfrac{1}{{\sqrt 2 }}$

The value of $k$ is $\dfrac{1}{{\sqrt 2 }}$

Note: Here given that one angle of the right angled triangle is ${45^ \circ }$, then we automatically understand that it is a right isosceles triangle. As to make the sum of the angles of a triangle ${180^ \circ }$, the other angle other than ${90^ \circ }$ angle is ${45^ \circ }$. Now as the two angles are equal, the two sides will also be equal other than the hypotenuse which is the property of the right isosceles triangle.