Solveeit Logo
Login

Question

Question: In a right-angled triangle ABC, if the hypotenuse \(AB=p\) , then what \[\overrightarrow{AB}\cdot \o...

In a right-angled triangle ABC, if the hypotenuse AB=pAB=p , then what AB→⋅AC→+BA→⋅BC→+CA→⋅CB→\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB} equals to
A. pp
B. p2{{p}^{2}}
C. 2p22{{p}^{2}}
D. p22\dfrac{{{p}^{2}}}{2}

Explanation

Solution

We have to find the value of AB→⋅AC→+BA→⋅BC→+CA→⋅CB→\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB} . From, the figure, AC→⊥CB→\overrightarrow{AC}\bot \overrightarrow{CB} , CA→⊥CB→\overrightarrow{CA}\bot \overrightarrow{CB} and using the rule of vectors, we will get CA→⋅CB→=0\overrightarrow{CA}\cdot \overrightarrow{CB}=0 . Substituting these values in AB→⋅AC→+BA→⋅BC→+CA→⋅CB→\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB} and after some rearrangements, use the using the triangle law of vector addition (AB→=AC→+CB→)\left( \overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB} \right) and the property a⋅→a→=∣a→∣2\overrightarrow{a\cdot }\overrightarrow{a}={{\left| \overrightarrow{a} \right|}^{2}} , the required value will be obtained.

Complete step by step answer:
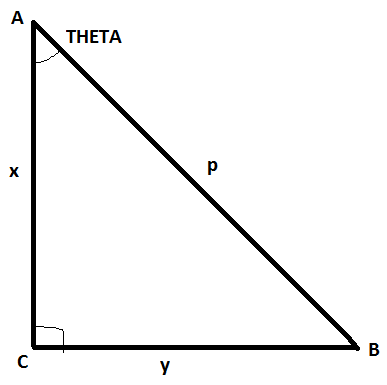
We have to find the value of AB→⋅AC→+BA→⋅BC→+CA→⋅CB→\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB} .

From the figure,
AC→⊥CB→\overrightarrow{AC}\bot \overrightarrow{CB}
And CA→⊥CB→\overrightarrow{CA}\bot \overrightarrow{CB}
We know that a→⋅b→=∣a→∣⋅∣b→∣⋅cos⁡θ\overrightarrow{a}\cdot \overrightarrow{b}=\left| \overrightarrow{a} \right|\cdot \left| \overrightarrow{b} \right|\cdot \cos \theta
⇒CA→⋅CB→=∣CA→∣⋅∣CB→∣cos⁡θ\Rightarrow \overrightarrow{CA}\cdot \overrightarrow{CB}=\left| \overrightarrow{CA} \right|\cdot \left| \overrightarrow{CB} \right|\cos \theta
This can be written as
CA→⋅CB→∣CA→∣⋅∣CB→∣=cos⁡θ\dfrac{\overrightarrow{CA}\cdot \overrightarrow{CB}}{\left| \overrightarrow{CA} \right|\cdot \left| \overrightarrow{CB} \right|}=\cos \theta
Given that the triangle is a right-angled triangle. Hence,
CA→⋅CB→∣CA→∣⋅∣CB→∣=cos⁡90=0\dfrac{\overrightarrow{CA}\cdot \overrightarrow{CB}}{\left| \overrightarrow{CA} \right|\cdot \left| \overrightarrow{CB} \right|}=\cos 90=0
This can be written as
CA→⋅CB→=0...(i)\overrightarrow{CA}\cdot \overrightarrow{CB}=0...(i)
Let us consider AB→⋅AC→+BA→⋅BC→+CA→⋅CB→\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+\overrightarrow{CA}\cdot \overrightarrow{CB}
Substituting (i)(i) in the above equation, we will get
AB→⋅AC→+BA→⋅BC→+0\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}+0
=AB→⋅AC→+BA→⋅BC→=\overrightarrow{AB}\cdot \overrightarrow{AC}+\overrightarrow{BA}\cdot \overrightarrow{BC}
We know that AB→=−BA→\overrightarrow{AB}=-\overrightarrow{BA} . So the above equation can be written as
AB→⋅AC→−AB→⋅BC→\overrightarrow{AB}\cdot \overrightarrow{AC}-\overrightarrow{AB}\cdot \overrightarrow{BC}
Taking AB→\overrightarrow{AB} common, we will get
AB→⋅(AC→−BC→)\overrightarrow{AB}\cdot \overrightarrow{(AC}-\overrightarrow{BC})
We know that BC→=−CB→\overrightarrow{BC}=-\overrightarrow{CB} . So the above equation can be written as
AB→⋅(AC→+CB→)...(ii)\overrightarrow{AB}\cdot \overrightarrow{(AC}+\overrightarrow{CB})...(ii)
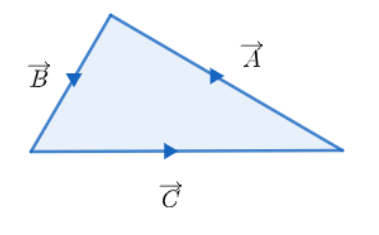
Using triangle law of vector addition, that is, for a triangle shown below, A→=B→+C→\overrightarrow{A}=\overrightarrow{B}+\overrightarrow{C}

Similarly, we can express the same for the given triangle. That is,
AB→=AC→+CB→\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}
Hence, (ii)(ii) can be written as
AB→⋅AB→\overrightarrow{AB}\cdot \overrightarrow{AB}
We know that a⋅→a→=∣a→∣2\overrightarrow{a\cdot }\overrightarrow{a}={{\left| \overrightarrow{a} \right|}^{2}}
Hence, AB→⋅AB→=∣AB→∣2\overrightarrow{AB}\cdot \overrightarrow{AB}={{\left| \overrightarrow{AB} \right|}^{2}}
=∣p∣2=p2={{\left| p \right|}^{2}}={{p}^{2}}

So, the correct answer is “Option B”.

Note: The students can make an error if they don’t know how to write the dot product of two vectors. Also, the property of vectors and triangular law of vector addition is also very important to solve this question and hence need to be very thorough in this. There can also be a chance to make error in the equation CA→⋅CB→∣CA→∣⋅∣CB→∣=cos⁡θ\dfrac{\overrightarrow{CA}\cdot \overrightarrow{CB}}{\left| \overrightarrow{CA} \right|\cdot \left| \overrightarrow{CB} \right|}=\cos \theta by writing sin⁡θ\sin \theta instead of cos⁡θ\cos \theta .