Question

In a right angle triangle ABC, right-angled at B, if $\tan A = 1$ then verify that $2\sin A\cos A = 1$.

Answer 1

Hint: Here, we will verify $2\sin A\cos A = 1$by finding the values of $\sin A$ and $\cos A$ with the given $\tan A$ value.

Complete step-by-step answer:
Given,
In a right angle triangle ABC, right-angled at B i.e..,$\angle ABC = {90^0}$

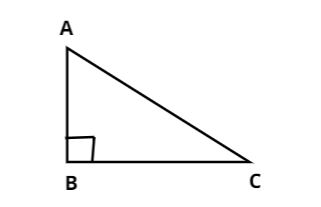
And it is also given that $\tan A = 1$i.e.., $\dfrac{{BC}}{{AB}} = 1[\because \tan \theta = \dfrac{{opp}}{{Adj}}]$.
Therefore, $BC = AB$
Let, $AB = BC = k$ where ‘k’ is a positive number.
As we know that $A{C^2} = A{B^2} + B{C^2}[\because$Pythagoras Theorem]
Now let us substitute the value of AB, BC as ‘k’, we get
$

\Rightarrow A{C^2} = {k^2} + {k^2} \\
\Rightarrow A{C^2} = 2{k^2} \\
\Rightarrow AC = \sqrt 2 k \\
$Now, let us find the value of$\sin A$and$\cos A$.$ \Rightarrow \sin A = \dfrac{{opp}}{{hyp}} = \dfrac{{BC}}{{AC}} = \dfrac{k}{{\sqrt 2 k}} = \dfrac{1}{{\sqrt 2 }}$$ \Rightarrow \cos A = \dfrac{{adj}}{{hyp}} = \dfrac{{AB}}{{AC}} = \dfrac{k}{{\sqrt 2 k}} = \dfrac{1}{{\sqrt 2 }}$Now, we need to verify$2\sin A\cos A = 1$.Let us substitute the obtained$\sin A$and$\cos A$values.$
\Rightarrow 2\sin A.\cos A = 1 \\
\Rightarrow 2(\dfrac{1}{{\sqrt 2 }})(\dfrac{1}{{\sqrt 2 }}) = 1 \\
\Rightarrow \dfrac{2}{2} = 1 \\
\Rightarrow 1 = 1[\therefore L.H.S = R.H.S] \\
$Therefore, we verified that the value of$2\sin A\cos A$ is 1.

Note: The alternate approach to solve the given problem is by using the formula of double angle i.e..,$2\sin A\cos A = \sin 2A = \dfrac{{2\tan A}}{{1 + {{\tan }^2}A}}$.