Question

In a rhombus ABCD, if AC = 10cm and BD = 24cm. Then find the perimeter of rhombus ABCD.

Answer 1

First of all we have to understand about rhombus and its perimeter.
Rhombus: In rhombus opposite sides are parallel and all sides are equals to each other and the opposite angles are equal. As from figure mentioned above, AB||DC and AD||BC and AB=BC=CD=DA
Perimeter of rhombus: The perimeter of rhombus is the total length of its boundaries. So, the formula of perimeter of rhombus as mentioned below:
Perimeter of rhombus = AB + BC + CD + DA……………………………….(A)
Now, we know that diagonals of rhombus cut together in equal parts and cut together at ${90^{^0}}$ so, $\Delta ADO$ is the right angle triangle
Pythagoras rule: It states for all right angle triangles, in which the square of the hypotenuse is equal to the sum of squares of the other two sides.
So, In the figure mentioned above we can use the Pythagoras rule to find the side of the rhombus.
Then, we can find the perimeter of the rhombus after finding the side of the rhombus.

Complete step by step answer:
Step 1: As, given in the question in rhombus ABCD are AC = 10cm and BD = 24cm as mentioned in the figure below:

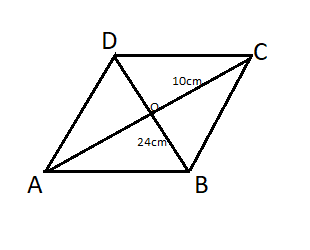
Step 2: We know that the diagonals of the rhombus are bisect each other at ${90^{^0}}$ so, $\Delta ADO$ is the right angle triangle and $OA = \dfrac{{AC}}{2}$ and $OD = \dfrac{{BD}}{2}$
Now, we can find the OA and OD as mentioned below:
$\Rightarrow OA = \dfrac{{10}}{2}$
$\Rightarrow OA = 5cm$
$\Rightarrow OD = \dfrac{{24}}{2} \\\ \Rightarrow OD = 12cm \\\$
Now, we can use the Pythagoras rule to find the side of the rhombus.
${\left( {AD} \right)^2} = {\left( {OA} \right)^2} + {\left( {OD} \right)^2}$…………………………..(1)
Step 3: Now, out the value of OA and OD in the above expression (1)
$\Rightarrow {\left( {AD} \right)^2} = {\left( 5 \right)^2} + {\left( {12} \right)^2} \\\ \Rightarrow {\left( {AD} \right)^2} = 25 + 144 \\\ \Rightarrow {\left( {AD} \right)^2} = 169 \\\ \Rightarrow \left( {AD} \right) = \sqrt {169} \\\ \Rightarrow AD = 13cm \\\$
Step 4: Now, we know that all sides of rhombus are equal to each other. So, we can use the formula of perimeter of rhombus (A) as mentioned in the solution hint.
Perimeter of rhombus = AB + BC + CD + DA
As, we know that the all sides are equals to each other
So, We can get
Perimeter of rhombus = DA + DA + DA + DA
Perimeter of rhombus = 13 + 13 + 13 + 13
Perimeter of rhombus = 52cm

In a rhombus ABCD, if AC = 10cm and BD = 24cm, the perimeter of rhombus is 52cm

Note: First of all we have to know about rhombus and its basic properties to find the side of rhombus.
Then, we have to use the Pythagoras rule to find the side of the rhombus.