Solveeit Logo
Login

Question

Question: In a regular hexagon ABCDEF, \(\overset{\rightarrow}{AE} =\)...

In a regular hexagon ABCDEF, AE→=\overset{\rightarrow}{AE} =

A

2a−3b2\mathbf{a} - 3\mathbf{b}

B

AC→+AF→−AB→\overset{\rightarrow}{AC} + \overset{\rightarrow}{AF} - \overset{\rightarrow}{AB}

C

AC→+AB→−AF→\overset{\rightarrow}{AC} + \overset{\rightarrow}{AB} - \overset{\rightarrow}{AF}

D

None of these

Answer

AC→+AF→−AB→\overset{\rightarrow}{AC} + \overset{\rightarrow}{AF} - \overset{\rightarrow}{AB}

Explanation

Solution

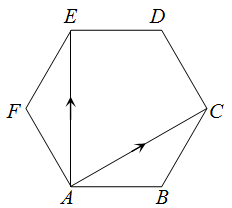
Obviously, AE→=AC→+CD→+DE→\overset{\rightarrow}{AE} = \overset{\rightarrow}{AC} + \overset{\rightarrow}{CD} + \overset{\rightarrow}{DE}

=AC→+AF→−AB→= \overset{\rightarrow}{AC} + \overset{\rightarrow}{AF} - \overset{\rightarrow}{AB}, {∵CD→=AF→andDE→=−AB→}\left\{ \because\overset{\rightarrow}{CD} = \overset{\rightarrow}{AF}\text{and}\overset{\rightarrow}{DE} = - \overset{\rightarrow}{AB} \right\}.