Question
Question: In a reference frame K, two particles travel along the x axis, one of mass $m_1$ with velocity $\vec...
In a reference frame K, two particles travel along the x axis, one of mass m1 with velocity v1, and the other of mass m2 with velocity v2. Another reference frame K' moves with a velocity v relative to K. If μ is the reduced mass of the particles, then:
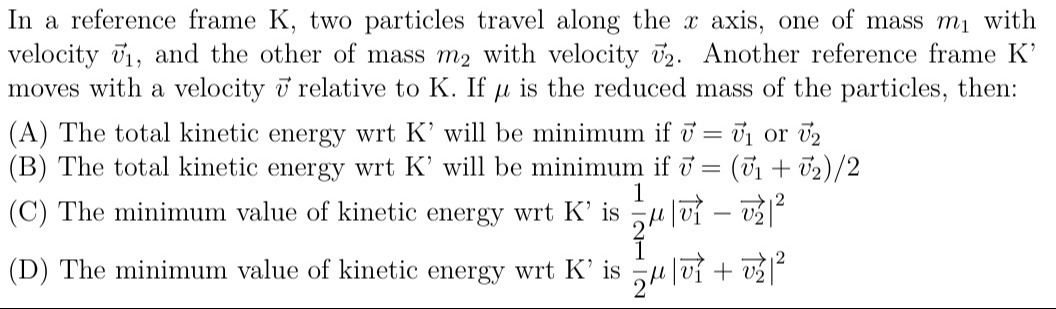
The total kinetic energy wrt K' will be minimum if v=v1 or v2
The total kinetic energy wrt K' will be minimum if v=(v1+v2)/2
The minimum value of kinetic energy wrt K' is 21μ∣v1−v2∣2
The minimum value of kinetic energy wrt K' is 21μ∣v1+v2∣2
The minimum value of kinetic energy wrt K' is 21μ∣v1−v2∣2
Solution
The kinetic energy of the two-particle system in frame K' is T′=21m1(v1−v)2+21m2(v2−v)2. To find the minimum kinetic energy, we differentiate T′ with respect to v (or its component, since motion is 1D) and set the derivative to zero. This yields v=m1+m2m1v1+m2v2, which is the velocity of the center of mass (vCM) of the system. Thus, the minimum kinetic energy occurs when K' is the center of mass frame. Substituting v=vCM back into the expression for T′ and simplifying, we get Tmin′=21m1+m2m1m2∣v1−v2∣2. Recognizing that μ=m1+m2m1m2 is the reduced mass, the minimum kinetic energy is 21μ∣v1−v2∣2.
