Question
Question: In a rectangle ABCD, M and N are the midpoint of the sides BC and CD respectively. If \[\overset\fro...
In a rectangle ABCD, M and N are the midpoint of the sides BC and CD respectively. If ANM⌢=90∘ then AB:BC is
A. 2:1
B. 2:1
C. 3:1
D. 1:1
Solution
Hint: Use trigonometric identities and find the relation between them. The relation cot and tan are important here, they are reciprocal of each other and the complement of tan is cot. Then put the values and solve if the square root is converted into the square from one said to another.
Complete step-by-step answer:
Let AB=DC=2x and AD=BC=2y.
In
tanθ=baseperpendicular
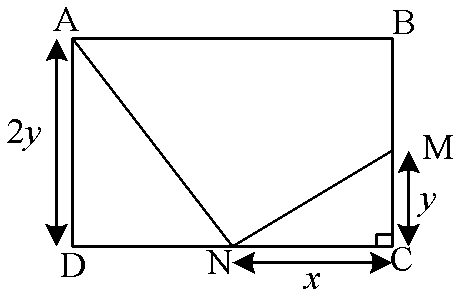
tanθ=xy … (1)
In ΔADN , tan(90−θ)=x2y …(2)
cotθ=x2y
tanθ=2yx \left\\{ as\,\,\cot \theta =\dfrac{1}{\tan \theta } \right\\}
By putting the value of from equation
xy=2yx.
x2=2y2
y2x2=12
(yx)2=12
(yx)=12.
The correct option is B.
Note: Firstly, draw the neat and clear diagram name every angle or side. Then write the given and what to find. Use Trigonometric identities and formulas to solve. Then solve the value of x and y according to the problems.
