Question

In a rectangle$ABCD$ ,$AB = 2l$ and$BC = l$. Axes $xx$ and $yy$ pass through the centre of the rectangle. The moment of inertia is least about:

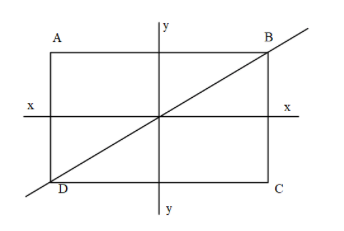
A) $BD$
B) $BC$
C) $xx$
D) $yy$

Answer 1

The moment of inertia depends upon the mass of the body and the square of the distance from the axis of the particles of the body, so we need to find the axis from which the distance of the particle will be least.

Complete Step by step solution:
It is given in the problem that in a rectangle$ABCD$ ,$AB = 2l$ and$BC = l$. Axes $xx$ and $yy$ pass through the centre of the rectangle and we need to find the axis at which the moment of inertia is minimum.
Here we can observe that the axis from which all the particles are at minimum distance is the axis xx.

The correct answer for this problem is option C.

Additional information: The parallel axis theorem is used to calculate the moment of inertia about an axis which is parallel about a given moment of inertia. $I = {I_c} + M{h^2}$,here$I$ is the moment of inertia about an axis which is parallel to ${I_c}$ and which is $h$ distance away from it. The moment of inertia can be defined as the ratio of torque to the angular acceleration. The moment of inertia is equal to the product of mass and square of radius of gyration, the radius of gyration is the distance from the axis of rotation to the point at which the body would have the same moment of gyration.

Note: It is advised to students to understand and remember the formula of the moment of inertia and also it is important for students to remember the moment of inertia of some standard bodies. The moment of inertia is defined as the ratio of the angular momentum and angular velocity.