Question

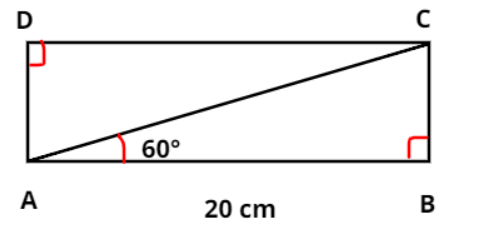
In a rectangle ABCD, AB = 20 cm, $\angle BAC = {60^ \circ }$ calculate side BC and diagonals AC, BD.

Answer 1

In this question we will be using some basic trigonometric formulas like $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ and ${\text{cos}}\theta = \dfrac{{Base}}{{Hypotenuse}}$also some basic properties of rectangles which can be used to approach the solution.

Complete step-by-step answer:
Given, ABCD is a rectangle, AB = 20 cm, $\angle BAC = {60^ \circ }$
From the figure, we can clearly see that $\Delta ABC$ is a right-angled triangle at vertex B
As in a right-angled triangle we know that the side opposite to right angle AC is hypotenuse, side opposite to the considered angle ($\angle BAC$) BC is perpendicular and the remaining side is base
Also, $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$and ${\text{cos}}\theta = \dfrac{{Base}}{{Hypotenuse}}$
In $\Delta ABC$ from the figure, we can write
$\tan \left( {\angle BAC} \right) = \dfrac{{BC}}{{AB}} = \dfrac{{BC}}{{20}}$
$\Rightarrow \dfrac{{BC}}{{20}} = \tan {60^ \circ }$
$\Rightarrow BC = 20\tan {60^ \circ }$
Since, $\tan {60^ \circ } = \sqrt 3$
$\Rightarrow BC = 20\sqrt 3 cm$
Length of side BC is $20\sqrt 3 cm$
Again from $\Delta ABC$, we can write
$\cos \left( {\angle BAC} \right) = \dfrac{{AB}}{{AC}} = \dfrac{{20}}{{AC}}$
$\Rightarrow \dfrac{{20}}{{AC}} = \cos {60^ \circ }$
$\Rightarrow AC = \dfrac{{20}}{{\cos {{60}^ \circ }}}$
Since, $\cos {60^ \circ } = \dfrac{1}{2}$
$\Rightarrow {\text{AC}} = \dfrac{{20 \times 2}}{1} = 40{\text{ cm}}$
Length of diagonal AC is 40 cm
Also, according to the properties of a rectangle we know that the diagonals of a rectangle are equal in length
Therefore, AC = BD = 40 cm
Hence, the length of both the diagonals AC and BD is 40 cm.

Note: These types of problems are simply solved with the help of the figure which can be drawn by considering the aspects of the problem. After that some basic geometry is applied to these problems and solved by simple trigonometric formulas.