Question

In a quark model of elementary particles, a neutron is made of one up quark of charge $\dfrac{2}{3}e$ and two down quarks of charges $\left( { - \dfrac{1}{3}e} \right)$. If they have a triangle configuration with side length of order ${10^{ - 15}}m$. The electrostatic potential energy of neutron in $MeV$ is:

Answer 1

The numerical problem given above can be solved easily by assuming the quarks to be the same as charged particles such as electrons. The three charged particles are arranged in a triangle arrangement.

Formula Used:
The mathematical formula for calculating electric potential energy is given as:
$U$ = $\dfrac{1}{{4\pi {\varepsilon_0}r}}\left[ {{q_u}{q_d} + {q_d}{q_d} + {q_d}{q_u}} \right]$
In this mathematical expression, $r =$ the distance between two quarks, ${q_u} =$charge in an up quark and ${q_d} =$charge in a down quark.

Complete step by step solution:
In the numerical problem given above the quarks are arranged in the form of an equilateral triangle as shown in the figure drawn below:

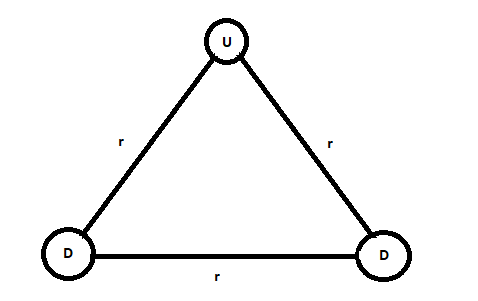
From the given numerical problem we know that the separation between the two charges is $r = {10^{ - 15}}m$.
Also the charge of an Up quark is given as ${q_u} = \dfrac{2}{3}e$
Similarly, the charge of a Down quark is given as ${q_d} = \left( { - \dfrac{1}{3}e} \right)$
Now we can substitute these values in the mathematical expression given above. Substituting these values we get:
U = \left[ {\dfrac{1}{{4\pi {\varepsilon _ \circ }r}}} \right] \times \left\\{ {\left( {\dfrac{2}{3}e} \right)\left( {\dfrac{{ - 1}}{3}e} \right) + {{\left( {\dfrac{{ - 1}}{3}e} \right)}^2} + \left( {\dfrac{{ - 1}}{3}e} \right)\left( {\dfrac{2}{3}e} \right)} \right\\}
When we calculate the value of this mathematical equation we get:
U = \left[ {\dfrac{1}{{4\pi {\varepsilon _ \circ }r}}} \right] \times \left\\{ {\dfrac{{ - {e^2}}}{3}} \right\\}
Now we know that $\dfrac{1}{{4\pi {\varepsilon _ \circ }}} = 9 \times {10^9}$, $r = {10^{ - 15}}$and $e = 1.6 \times {10^{ - 19}}$. We can put these values in the above equation. Thus, we get:
$U = \dfrac{{9 \times {{10}^9}}}{{{{10}^{ - 15}}}}\left[ {\dfrac{{ - {{\left( {1.6 \times {{10}^{ - 19}}} \right)}^2}}}{3}} \right]$
Solving this we get:
$U = - 7.68 \times {10^{ - 14}}J$
But this value of electrostatic potential energy of the neutron is given in Joules but we have to calculate the value in Mega-electron Volts. Thus we have to convert the unit to $MeV$
We know that $1J = 6.4 \times {10^{12}}MeV$. Using this to convert the equation.
Thus, $U = - 0.48MeV$

Hence, we find that the electrostatic potential energy of the neutron in $MeV$ is equal to $- 0.48MeV$.

Note: It is important to be very careful while solving numerical problems of this type as the calculations tend to get very tedious and time consuming. Even if a minor mistake is made in any step it could affect the final result.