Question

In a quark model of elementary particles, a neutron is made of one up quark of charge$\dfrac{2}{3}e$ and two down quark of charges$\left( -\dfrac{1}{3}e \right)$. If they have a triangle configuration with a side length of the order of ${{10}^{-15}}m$. The electrostatic potential energy of the neutron in MeV is:
A. 7.68
B. -5.21
C. -0.48
D. 9.34

Answer 1

The potential energy of the given equilateral triangular system with 3 charges (the quarks are considered to be as the charges) can be obtained as the algebraic sum of the potential energies of each pair. Here, we get 3 pairs, 1 pair is down quark and down quark and the other 2 pairs are of up quark and down quark.

Complete step by step answer:
From the given information, we have the data as follows.
The total number of up quarks for neutron, 1
The total number of down quarks for neutron, 2
The charge on an up quark, $\dfrac{2}{3}e$
The charge on a down quark, $\dfrac{1}{3}e$
The distance between each quark, ${{10}^{-15}}m$
The quarks are arranged on the vertices of an equilateral triangle with a side of ${{10}^{-15}}m$. The potential energy between the 2 charges is given by the formula as follows.
$U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{r}$
Where ${{q}_{1}},{{q}_{2}}$are the charges and r is the distance between them.
Consider the diagram representing the given information.

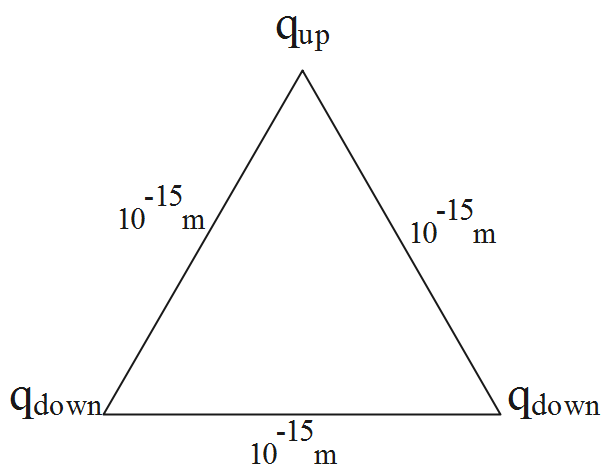
The potential energy of the given equilateral triangular system with 3 charges (the quarks are considered to be as the charges) can be obtained as the algebraic sum of the potential energies of each pair.
The formula representing the same is given as follows.
$U=\dfrac{1}{4\pi {{\varepsilon }_{0}}}e\dfrac{\left[ {{q}_{down}}{{q}_{down}}+{{q}_{down}}{{q}_{up}}+{{q}_{down}}{{q}_{up}} \right]}{r}$
Substitute the values in the above formula.
$U=\dfrac{\left( 9\times {{10}^{9}} \right){{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{{{10}^{-15}}}\left[ \dfrac{-1}{3}\left( \dfrac{-1}{3} \right)-\dfrac{2}{3}\left( \dfrac{1}{3} \right)-\dfrac{2}{3}\left( \dfrac{1}{3} \right) \right]$
Continue further computation.

& U=2.304\times {{10}^{-13}}\left[ \dfrac{1}{9}-\dfrac{2}{9}-\dfrac{2}{9} \right] \\\ & \Rightarrow U=2.304\times {{10}^{-13}}\left[ -\dfrac{3}{9} \right] \\\ \end{aligned}$$ The potential energy in terms of the Joules is $$\therefore U=-7.68\times {{10}^{-14}}J$$ In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on the electron, so, we have, $$U=-\dfrac{7.68\times {{10}^{-14}}}{1.6\times {{10}^{-19}}}eV$$ Thus, the value of the potential energy in terms of MeV is, $$\therefore U=-0.48\,MeV$$ **So, the correct answer is “Option C”.** **Note:** The quarks are considered to be charges, as they carry some energy. In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on an electron. This conversion method should be known to get the final answer.