Solveeit Logo
Login

Question

Question: In a quadrilateral PQRS, M and N are midpoints of the sides PQ and RS resepectively. If PS + QR = tM...

In a quadrilateral PQRS, M and N are midpoints of the sides PQ and RS resepectively. If PS + QR = tMN then t =

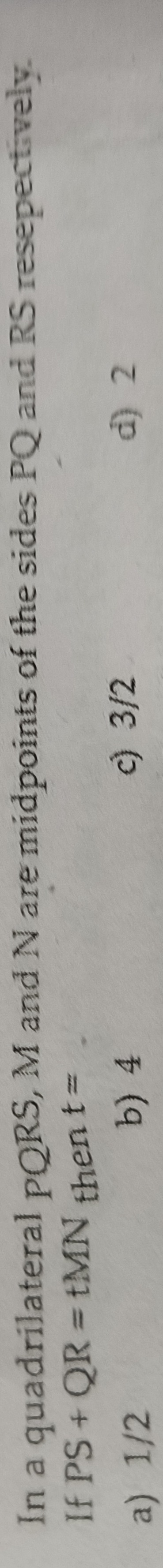
A

1/2

B

4

C

3/2

D

2

Answer

2

Explanation

Solution

Let the position vectors of P,Q,R,SP, Q, R, S be P⃗,Q⃗,R⃗,S⃗\vec{P}, \vec{Q}, \vec{R}, \vec{S} respectively.

  • The midpoints: M⃗=P⃗+Q⃗2,N⃗=R⃗+S⃗2\vec{M} = \frac{\vec{P} + \vec{Q}}{2}, \quad \vec{N} = \frac{\vec{R} + \vec{S}}{2}
  • Thus, MN⃗=N⃗−M⃗=R⃗+S⃗−P⃗−Q⃗2=(R⃗−P⃗)+(S⃗−Q⃗)2\vec{MN} = \vec{N} - \vec{M} = \frac{\vec{R} + \vec{S} - \vec{P} - \vec{Q}}{2} = \frac{(\vec{R} - \vec{P}) + (\vec{S} - \vec{Q})}{2}
  • Now, observe that: PS⃗=S⃗−P⃗andQR⃗=R⃗−Q⃗\vec{PS} = \vec{S} - \vec{P} \quad \text{and} \quad \vec{QR} = \vec{R} - \vec{Q}
  • Adding these, PS⃗+QR⃗=(S⃗−P⃗)+(R⃗−Q⃗)=(R⃗−P⃗)+(S⃗−Q⃗)=2MN⃗.\vec{PS} + \vec{QR} = (\vec{S} - \vec{P}) + (\vec{R} - \vec{Q}) = (\vec{R} - \vec{P}) + (\vec{S} - \vec{Q}) = 2\vec{MN}.
  • Given PS+QR=t MNPS + QR = t\,MN, it follows that: t MN=2 MN  ⟹  t=2.t\,MN = 2\,MN \implies t = 2.