Question
Question: In a projectile motion, KE varies with time as in graph: (\[\theta \ne 0^\circ ,180^\circ \] with ve...
In a projectile motion, KE varies with time as in graph: (θ=0∘,180∘ with vertical)
A. 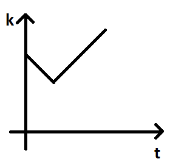
B. 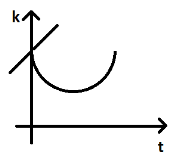
C. 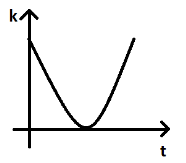
D. 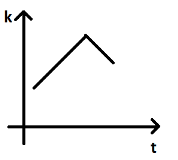
Solution
To solve this problem, we need to know the changes taking place in the kinetic energy of a projectile with respect to time when it is projected with a certain velocity. We will also use the fact that the total energy of the projectile is the sum of its kinetic energy and potential energy. According to this, we will eliminate the wrong options one by one and finally get the final answer.
Formulas used:
KE=21mv2,
where, KE is kinetic energy, m is mass and v is velocity.
PE=mgh, where, PE is potential energy, m is mass, g is gravitational acceleration and h is height.
Complete step by step answer:
We know that the kinetic energy of the body decreases and the potential energy increases when the body is projected with some velocity. Here, in option D it is shown that initially the kinetic energy increases with time which is not correct. Thus, option D cannot be our answer.
When the body is projected with the velocity v, the minimum velocity is vcosθ which is the horizontal component of velocity. This is not equal to zero. Therefore, kinetic energy will never be zero. Thus, option C cannot be our answer.
Now, we know that total energy is the sum of kinetic energy and potential energy.
Here, we know that total energy of the body remains constant.
And potential energy PE=mgh
Where, h=vsinθ⋅t−21gt2.
Thus potential energy is a quadratic function of time and hence the kinetic energy also changes quadratically with respect to time.In option A, it is shown that kinetic energy varies linearly with respect to time which is incorrect. Thus, option A cannot be our answer.
Hence, option B is the right answer.
Note: We have seen how kinetic energy changes with respect to time in a projectile motion. We have considered two important facts here. First is that the minimum velocity of the projectile in motion is equal to the horizontal component of the velocity and not zero. Another important thing is that the potential energy is the quadratic function of time which makes the same for the kinetic energy.
