Question
Question: In a portion of some large electrical network, current in certain branches are known. The values of ...
In a portion of some large electrical network, current in certain branches are known. The values of VAVB and VCVD are and X and Y respectively, where X and Y are:
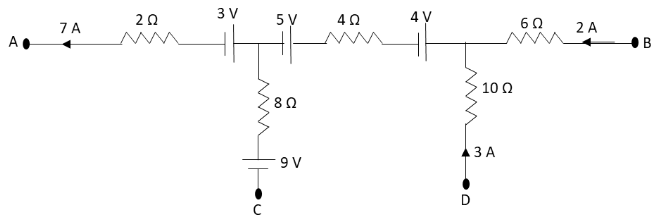
A. X=29V,Y=26V
B. X=58V,Y=52V
C. X=−58V,Y=−52V
D. X=−29V,Y=−26V
Solution
Determine the value of the electric current flowing from the branch at point C using Kirchhoff’s current law. Then apply Kirchhoff’s voltage law to the electrical network between the points A and B and C and D to determine the potential difference between points A and B and the points C and D.
Complete step by step answer:
We have given a large electrical network in which there are various resistors, currents flowing and batteries. We have asked to determine the potential difference between the points A and B and the potential difference between the points C and D.
Let us redraw the given electrical network with all the electric current values shown in the network.
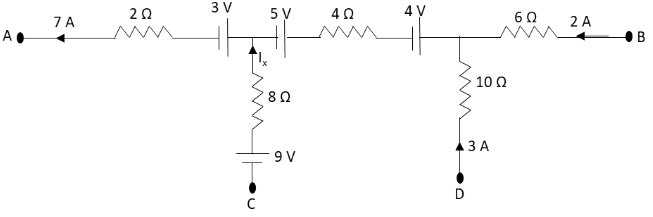
Let us first determine the value of the electric current Ix in the above electrical network. Let us apply Kirchhoff’s current law to the given electrical network.
7A=2A+3A+Ix
⇒7A=5A+Ix
⇒Ix=7A−5A
⇒Ix=2A
Hence, the current entering the branch of the given network is 2A.
To determine the potential difference between the points A and B of the given electrical network, we should apply Kirchhoff voltage law between the points A and B.
VA−(7A)(2Ω)−(3V)−(5V)−(3A+2A)(4Ω)−(4V)−(2A)(6Ω)−VB=0
Here, VA is the potential at point A and VB is the potential at point B.
⇒VA−14−3−5−20−4−12−VB=0
⇒VA−58−VB=0
⇒VA−VB=58V
Therefore, the potential difference between the points A and B is 58V. Hence, the determined value of X is 58V.
X=58V
To determine the potential difference between the points A and B of the given electrical network, we should apply Kirchhoff voltage law between the points A and B.
VC−(9V)+(2A)(8Ω)−(5V)−(3A+2A)(4Ω)−(4V)−(3A)(10Ω)−VD=0
Here, VC is the potential at point B and VD is the potential at point D.
⇒VC−9+16−5−20−4−30−VD=0
⇒VC−52−VD=0
⇒VC−VD=52V
Therefore, the potential difference between the points C and D is 52V. Hence, the determined value of Y is 52V.
∴Y=52V
Hence, the correct option is B.
Note: The students should not forget to determine the electric current originating from branch at point C in the given electrical network. If this current value is not used while applying Kirchhoff’ voltage and current law, then the final values of the potential differences will be incorrect.
