Question

In a population study of 1500 Indian rivers, the following data were reported. $520$ were polluted by sulphur compounds, $335$ polluted by phosphate, $425$ were polluted by crude oil, $100$ were polluted by both crude oil and sulphur compounds, $180$ were polluted by both sulphur compounds and phosphates, $150$ were polluted by both phosphates and crude oil and $28$ were polluted by sulphur compounds, phosphates and crude oil. How many of the rivers were polluted by exactly one of the three impurities.

Answer 1

We need to draw a proper Venn diagram to analyse the question. Form an equation and do some calculation and then we will calculate the values in empty spaces. Finally we get the required answer.

Formula used:

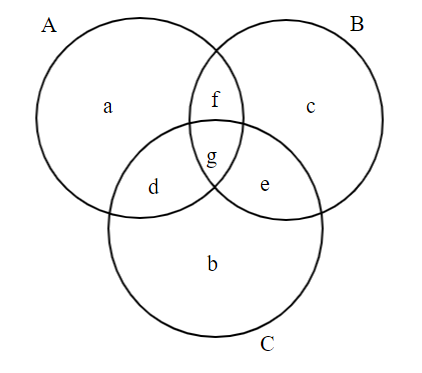
For the above Venn diagram:
Sum of exactly one is $=$ $(a + b + c)$.
Both $A$ and $C$ is $= (d + g).$
Both $A$ and $B$ is $= (f + g).$
Both $B$ and $C$ is $= (e + g).$
And, all of $A,B$ and $C$ is$= g$.
Total in $A$ is $= (a + f + g + d).$
Total in $B$ is $= (c + f + g + e).$
Total in $C$ is $= (b + d + g + e).$

Complete step-by-step solution:
Now, if we plot the given question in the above Venn diagram, we get the following picture:

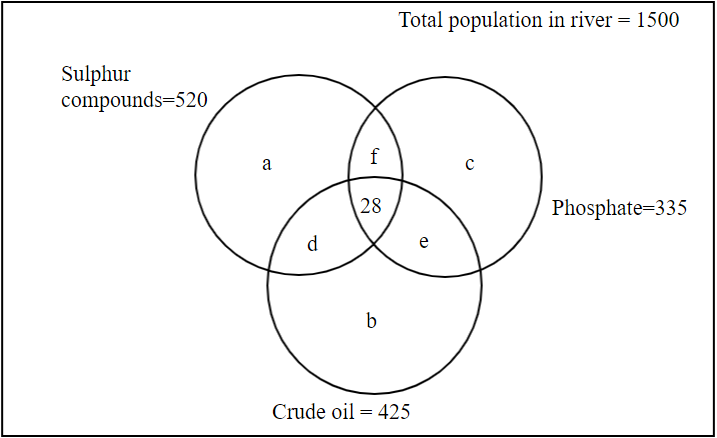
In the question, it is given that:
Pollution made by Sulphur compounds $= 520.$
Pollution made by phosphates$= 335$.
Pollution made by crude oil$= 425$.
So, from the above diagram we can say that:
$(a + d + f + 28) = 520$.
$(b + d + e + 28) = 425$.
$(c + f + e + 28) = 335$.
But, it is also said that: $100$ people were polluted by both crude oil and sulphur compounds.
So, $d + 28 = 100.$
$\Rightarrow d = 100 - 28 = 72.$
Again,$180$ people were polluted by both sulphur compounds and phosphates.
So, $f + 28 = 180.$
$\Rightarrow f = 180 - 28 = 152.$
Again, $150$ people were polluted by both phosphates and crude oil.
So, $e + 28 = 150.$
$\Rightarrow e = 150 - 28 = 122.$
By solving the above equations, we get that:
$a + d + f + 28 = 520$
Putting the values and we get
$\Rightarrow a + 72 + 152 + 28 = 520$
Let us add the LHS and we get,
$\Rightarrow a + 252 = 520$
On subtracting $252$ on both sides we get
$\Rightarrow a = 520 - 252$
Let us subtract we get
$\Rightarrow a = 268.$
So, $268$ people were polluted by only sulphur compounds.
Again, $b + d + e + 28 = 425$
Putting the values and we get,
$\Rightarrow b + 72 + 122 + 28 = 425$
Let us add the LHS we get
$\Rightarrow b + 222 = 425$
Let us subtract $\;222$ on both sides we get,
$\Rightarrow b = 425 - 222$
On subtracting we get
$\Rightarrow b = 203.$
So, $203$ people were polluted by only crude oil.
Again, $c + f + e + 28 = 335$
Putting the values and we get,
$\Rightarrow c + 152 + 122 + 28 = 335$
Let us add the LHS we get,
$\Rightarrow c + 302 = 335$
On subtracting $302$ on both side we get,
$\Rightarrow c = 335 - 302$
So, $33$ people were polluted by only phosphates.
So, if we add the value of $a,b$ and$c$, we will get the number of people who are affected by exactly one of the three impurities
So,$(a + b + c) = 268 + 203 + 33 = 504.$

$\therefore$ $504$ people of the rivers were polluted by exactly one of the three impurities.

Note: A few points to remember:
If the data has given on two of the attributes among the three attributes, then we need consider the common part made by both the attributes.
Addition of the numbers in every uncovered part will give the total in a particular attribute in the Venn diagram.
Make sure that values of each variable are calculated properly.
Also, we can use union operations to solve this type of problems.