Question

In a pollution study of 1500 Indian rivers, the following data were reported. 520 were polluted by sulphur compounds, 335 polluted by phosphate, 425 were polluted by crude oil, 100 were polluted by both crude oil and sulphur compounds, 180 were polluted by both sulphur compounds and phosphates, 150 were polluted by both phosphates and crude oil and 28 were polluted by sulphur compounds, phosphates, and crude oil. How many of the rivers were polluted by exactly one of the three impurities.

Answer 1

To solve this problem we will make the venn diagram of the given data then we will use required union and intersection operations on the data by observing the venn diagram. As we need to find the number of rivers that are polluted by exactly one of the three given impurities we will find the number of rivers that are polluted only by one each impurities out of three and then add them all to get the answer.

Complete step by step answer:
We will make the venn diagram of the given data in the question to solve it,

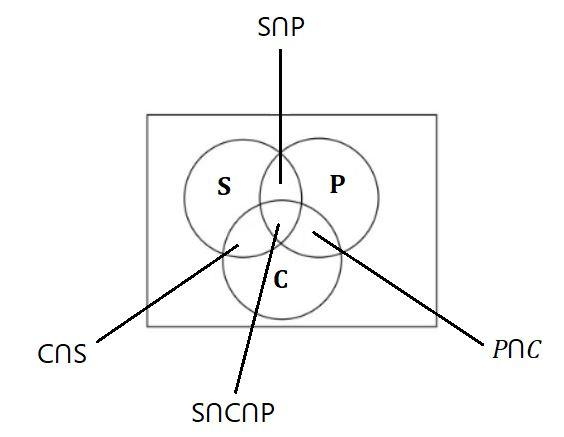
In the above diagram,
S represents the rivers polluted by sulphur compounds,
P represents the rivers polluted by phosphorous,
C represents the rivers polluted by crude oil.
And suppose U is the collection of all Indian rivers.
Now, we have
n(U) = 1500, n(S) = 520, n(P) = 335, n(C) = 425

Now, we are also given

& n(S\cap P)=180 \\\ & ,n(C\cap S)=100, \\\ & n(P\cap C)=150, \\\ & n(C\cap P\cap S)=28 \\\ \end{aligned}$$ And from the venn diagram, the number of rivers polluted by sulphur compound only is given by, $$n\left( S \right)-n\left( C\cap S \right)-n\left( S\cap P \right)+n\left( S\cap C\cap P \right)$$ = 520 – 100 – 180 + 28 = 268 And the number of rivers polluted by phosphate compound only we get as, $$n\left( P \right)-n\left( C\cap P \right)-n\left( S\cap P \right)+n\left( S\cap C\cap P \right)$$ = 335 – 150 – 180 + 28 = 33 From the venn diagram, the number of rivers polluted by crude oil only is given by, $$n\left( C \right)-n\left( C\cap S \right)-n\left( P\cap C \right)+n\left( S\cap C\cap P \right)$$ = 425 – 100 – 150 + 28 = 203 And hence to get the total number of rivers polluted by only 1 of the three impurities we will add all the above data so we get, total number of rivers polluted by only 1 of the three impurities = 268 + 33 + 203 = 504 Hence we get our answer as 504. **Note:** This problem is quite lengthy so you need to solve these kinds of problems step by step otherwise you may skip a step and end up with the wrong answer. And you need to make a venn diagram and observe it carefully before solving these kinds of problems without that you will not be able to solve it easily.