Solveeit Logo
Login

Question

Question: In a plot of log k vs \(\dfrac{1}{T}\) the slope is: (a)- \(\dfrac{-{{E}_{a}}}{2.303}\) (b)- \(...

In a plot of log k vs 1T\dfrac{1}{T} the slope is:
(a)- −Ea2.303\dfrac{-{{E}_{a}}}{2.303}
(b)- Ea2.303R\dfrac{{{E}_{a}}}{2.303R}
(c)- Ea2.303\dfrac{{{E}_{a}}}{2.303}
(d)- −Ea2.303R\dfrac{-{{E}_{a}}}{2.303R}

Explanation

Solution

The equation called Arrhenius equation is usually written as k=Ae−Ea/RTk=A{{e}^{-{{E}_{a}}/RT}} where the pre-exponential factor A is a constant and is called frequency factor andEa{{E}_{a}} is called the activation energy, R is the gas constant and T is the temperature. The activation energy is calculated by the formula log⁡k2k1=Ea2.303R[T2−T1T2T1]\log \dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right] where k1 and k2{{k}_{1}}\text{ and }{{k}_{2}} are rate constants at different temperatures.

Complete step by step answer:
The Arrhenius equation is usually written ask=Ae−Ea/RTk=A{{e}^{-{{E}_{a}}/RT}}.
And its log form is:
log⁡k2k1=Ea2.303R[T2−T1T2T1]\log\dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right]
To test the validity of the Arrhenius equation, let us consider the equation as:

ln⁡k=−EaRT+ln⁡A\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A
Or it can be converted into:
log⁡k=−Ea2.303RT+log⁡A\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A
This equation can be written in the form of the equation of the straight line.
The equation of the straight line is: y=mx + cy=mx\text{ + }c
So, in the straight line equation, when we plot a graph between y and x, we get m as the slop.
Similarly when we plot the graph for the equation log⁡k=−Ea2.303RT+log⁡A\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A:
log⁡k\log k is the y and 1T\dfrac{1}{T}is the x, the validity of the equation is confirmed.
So, when we plot the graph we get m = −Ea2.303R\dfrac{-{{E}_{a}}}{2.303R}
So, the slope of the line = −Ea2.303R\dfrac{-{{E}_{a}}}{2.303R}
The graph of log k vs 1T\dfrac{1}{T} is given below:


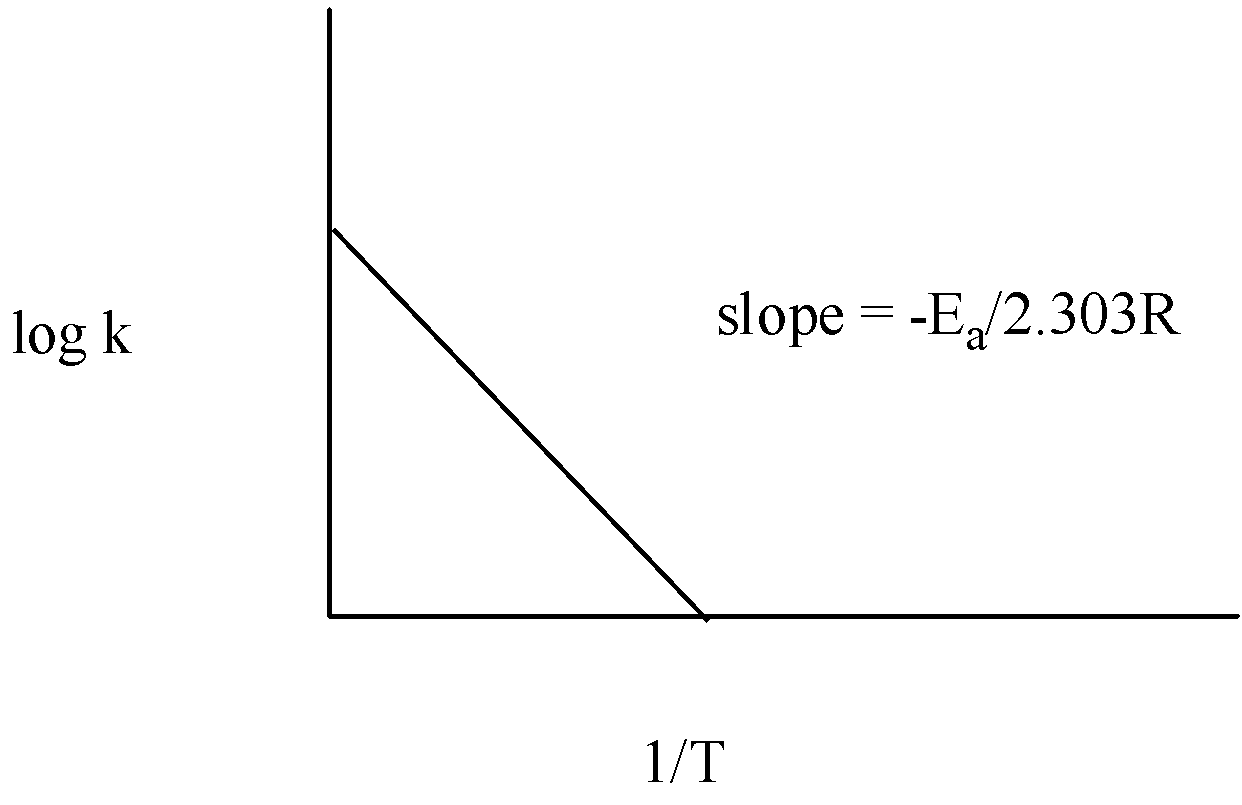
Thus, measuring the slope of the line, the value of Ea{{E}_{a}} can be calculated.
So, the correct answer is “Option D”.

Note: If we plot a straight line graph for the equation ln⁡k=−EaRT+ln⁡A\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A, the y will be ln k and the x will be 1T\dfrac{1}{T} so in this case we get the slope of−EaR-\dfrac{{{E}_{a}}}{R}. so, by converting any equation to the straight-line equation we can find the slope of the equation.