Question

In a plane there are two families of lines $y=x+r,$ $y=-x+r,$ where $r\in 0,1,2,3,4.$ The number of squares of diagonals of the length 2 units formed by the lines is

Answer 1

We solve this question by first using the given values of r in the above two equations. That way, we get 5 lines each for the two equations which specify the family of lines. We represent this graphically and next we find the distance between two lines. This gives us the length for the side of a square and using this, we find the squares whose diagonal length is given by 2 units.

Complete step-by-step solution:
In order to solve this question, let us consider the equations for the family of lines given in the question which are,
$\Rightarrow y=x+r$
$\Rightarrow y=-x+r$
Now, we are given that the values of r belong to the set of values 0, 1, 2, 3, 4. Substituting these in the above two equations, we get two sets of 5 lines for the two families of equations. The first family of lines are given as $y=x,y=x+1,y=x+2,y=x+3,y=x+4.$ The second family of lines are given as $y=-x,y=-x+1,y=-x+2,y=-x+3,y=-x+4.$ We now plot these lines on the graph as shown in the figure below.

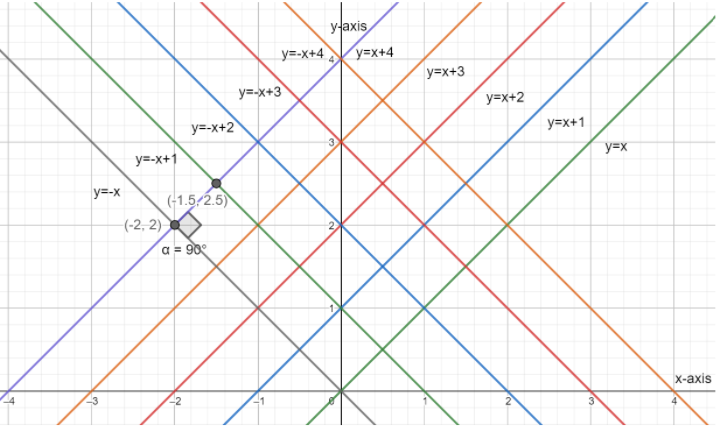
Looking at the figure, we can observe that the two families of lines are perpendicular to each other and their angle of intersection is given by $90{}^\circ$ as shown. Now, in order to find out the length of the diagonal, we first calculate the length of the side of the square given by the two points $\left( -2,2 \right)$ and $\left( -1.5,2.5 \right)$ using the distance formula $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}.$ Here, $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ represent the points $\left( -2,2 \right)$ and $\left( -1.5,2.5 \right)$ .
Substituting these values, we get
$\Rightarrow d=\sqrt{{{\left( -1.5-\left( -2 \right) \right)}^{2}}+{{\left( 2.5-2 \right)}^{2}}}$
Simplifying the terms in the brackets by subtracting,
$\Rightarrow d=\sqrt{{{\left( 0.5 \right)}^{2}}+{{\left( 0.5 \right)}^{2}}}$
We can represent 0.5 as $\dfrac{1}{2},$
$\Rightarrow d=\sqrt{{{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{1}{2} \right)}^{2}}}$
Squaring the terms,
$\Rightarrow d=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}$
Adding the two terms,
$\Rightarrow d=\sqrt{\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}$
This is the length for the side of the small square as shown in the figure. The length of its diagonal can be calculated using the formula $D=\sqrt{2}.d,$ where d is the length of one side of the square.
Using this formula, we can find the length of the diagonal of one square as,
$\Rightarrow D=\sqrt{2}.\dfrac{1}{\sqrt{2}}=1$
We are required to calculate the number of squares with diagonals of length 2 units each. In order to do so, we require the length of the diagonal to be twice the one calculated. This can be done by considering a square with a side length of $\dfrac{2}{\sqrt{2}}$ which is equal to $\sqrt{2}.$ This means that we need the square side length to be two times the original square length. This is done by taking two adjacent squares for a side length of $\sqrt{2}$ units. Therefore, taking four squares at a time, forming a bigger square, we get the diagonal length to be 2 units.
Hence, we are required to count the number of 4 such squares in the given squares. This is found to be 9. Hence, we have 9 such squares whose diagonals are of the length 2 units formed by the given lines.

Note: We need to count the squares properly. We can let the squares be overlapping. Without overlapping we get 4 squares which will give us a wrong answer. We need to consider overlapping in order to obtain the right answer.