Question

In a parallel RC circuit, there is $100\,mA$ through the resistive branch and $100\,mA$ through the capacitive branch. Find the total rms current.
A. $200\,mA$
B. $100\,mA$
C. $282\,mA$
D. $141\,mA$

Answer 1

Hint- For a parallel RC circuit the resistance and capacitor will be connected parallel to each other. Let the current through the resistive branch be ${I_R}$ and current through the capacitive branch be ${I_C}$ .Total current $I$ splits into ${I_R}$ and ${I_C}$. The relation between RMS current and peak current is given as
${I_{rms}} = \dfrac{{{I_0}}}{{\sqrt 2 }}$
Where ${I_{rms}}$ is RMS current and ${I_0}$ is the peak current
Using this we can find the value of total rms current in the given circuit.

Step by step solution:
A parallel RC circuit is a circuit in which the resistance and capacitor are connected parallel to each other. Since they are connected in parallel voltage across both resistor and capacitor will be equal.
But the current flowing through the resistive branch and capacitive branch will be different.

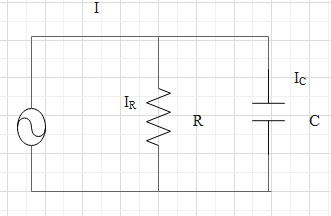
Given the current through the resistive branch is
${I_R} = 100\,mA$
Current through the capacitive branch is
${I_C} = 100\,mA$
From the figure we can see that total current $I$ splits into ${I_R}$ and ${I_C}$ .
hence total current in the circuit can be found out by adding current in the resistive branch and current in the capacitive branch.
Thus, we can write,
$I = {I_R} + {I_C}$
Let us substitute the value of current in the resistive branch and capacitive branch in the above equation to find the total current.
$I = 100\,mA + 100\,mA$
$\therefore I = 200\,mA$
We are asked to find the RMS current.
The relation between RMS current and peak current is given as
${I_{rms}} = \dfrac{{{I_0}}}{{\sqrt 2 }}$
Where ${I_{rms}}$ is RMS current and ${I_0}$ is the peak current
On substituting the value of peak current, we get
${I_{rms}} = \dfrac{{200\,mA}}{{\sqrt 2 }}$
$\therefore {I_{rms}} = 141\,mA$

So, the answer is option D

Note: In the question RMS value of current is asked. When we add the given values of current through resistor and current through capacitor what we get is the peak current always remember to convert it into RMS current by dividing it by $\sqrt 2$ .