Question

In a parabola ${{y}^{2}}=4ax$, find the locus of the poles of all chords of constant length 2c.
(a) $\left( {{y}^{2}}-4ax \right)\left( {{y}^{2}}+4{{c}^{2}} \right)=4{{a}^{2}}{{c}^{2}}$
(b) $\left( {{y}^{2}}-4ax \right)\left( {{y}^{2}}+4{{a}^{2}} \right)=8{{a}^{2}}{{c}^{2}}$
(c) $\left( {{y}^{2}}-4ax \right)\left( {{y}^{2}}+4{{c}^{2}} \right)=2{{a}^{2}}{{c}^{2}}$
(d) $\left( {{y}^{2}}-4ax \right)\left( {{y}^{2}}+4{{a}^{2}} \right)=4{{a}^{2}}{{c}^{2}}$

Answer 1

Hint:At first consider a point (h, k) on the pole of the chord, the equation of polar be with repetition to parabola be $yk=2a\left( x+h \right)$. Let that be intersect to parabola at $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$. Assure the distance between $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ and equate it with 2c to get master equation. Then from parabola’s and polar equation find the relation between ${{y}_{1}}$ and ${{y}_{2}}$ and put it in the master equation.

Complete step-by-step answer:
In the question we are given a parabola ${{y}^{2}}=4ax$ and we have to find the locus of the poles of all the chords of constant length 2c.
Now we are given the equation of parabola which is ${{y}^{2}}=4ax$.
Let’s suppose a point (h, k) is at the pole of the chord of length 2c.

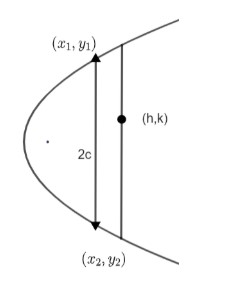
So to find the equation of polar of (h, k) with respect to parabola is,
$yk=2a\left( x+h \right)$
Now we say that let the polar intersect at parabola at $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$.
Also, we know that length of chord is constant that is 2c.
As the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ lie on parabola. So they should satisfy the equation of parabola ${{y}^{2}}=4ax$. So, we can write, $y_{1}^{2}=4a{{x}_{1}}$ and $y_{2}^{2}=4a{{x}_{2}}$.
Hence, ${{x}_{1}}$ is equal to $\dfrac{y_{1}^{2}}{4a}$ and ${{x}_{2}}$ is equal to $\dfrac{y_{2}^{2}}{4a}$.
As the length of the chord is given as 2c and its end points are also known $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$. So by using distance formula we can write,
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}=c$
So, now putting ${{x}_{1}}$ as $\dfrac{y_{1}^{2}}{4a}$ and ${{x}_{2}}$ as $\dfrac{y_{2}^{2}}{4a}$. So, we get,
$\sqrt{{{\left( \dfrac{y_{1}^{2}}{4a}-\dfrac{y_{2}^{2}}{4a} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}=2c$
Now on squaring both the sides we get,
${{\left( \dfrac{y_{1}^{2}}{4a}-\dfrac{y_{2}^{2}}{4a} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}=4{{c}^{2}}$
Now we know that, $y_{1}^{2}-y_{2}^{2}$ is $\left( {{y}_{1}}+{{y}_{2}} \right)\left( {{y}_{1}}-{{y}_{2}} \right)$. So, we can write,
$\dfrac{{{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}{{{\left( 4a \right)}^{2}}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}=4{{c}^{2}}$
Or, {{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}\left\\{ \dfrac{{{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}}{{{\left( 4a \right)}^{2}}}+1 \right\\}=4{{c}^{2}}
Let the above equation be considered as (i).
Now as we know that the equation of polar is $yk=2a\left( x+h \right)$. We can rewrite the equation as,
$x=\dfrac{yk}{2a}-h$
Now we will substitute x as $\dfrac{yk}{2a}-h$ in the equation of parabola. So, we get,
${{y}^{2}}=4ax=4a\left( \dfrac{yk}{2a}-h \right)$
So, ${{y}^{2}}=2yk-4ah$
Hence, ${{y}^{2}}-2yk+4ah=0$
In the equation the roots are ${{y}_{1}}$ and ${{y}_{2}}$. So, we can use the fact that the sum of the roots is equal to $\dfrac{\text{coefficient of y}}{\text{coefficient of}\, y^2}$. Here co – efficient of ${{y}^{2}}$ is 1 and that of y is -2k.
So, we can write that,
${{y}_{1}}+{{y}_{2}}=-\left( \dfrac{-2k}{1} \right)=2k$
Also, by the relation we can also say that product of roots is $\dfrac{\text{constant of the equation}}{\text{coefficient of}\, y^2}$. Here constant is $4ah$ and co – efficient of ${{y}^{2}}$ is 1.
So, ${{y}_{1}}{{y}_{2}}=4ah$
Now we know the value of ${{y}_{1}}+{{y}_{2}}$ and ${{y}_{1}}{{y}_{2}}$ which is 2k and 4ah respectively we can find value of ${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}$ by using the relation that, ${{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab$.
Here a is ${{y}_{1}}$ and b is ${{y}_{2}}$ so we get,
${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}={{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}-4{{y}_{1}}{{y}_{2}}$
Now substituting ${{y}_{1}}+{{y}_{2}}$ as 2k and ${{y}_{1}}{{y}_{2}}$ as 4ah we get,
${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}={{\left( 2k \right)}^{2}}-4\left( 4ah \right)$
Or, ${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}=4{{k}^{2}}-16ah$
So, ${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}=4\left( {{k}^{2}}-4ah \right)$
Now let’s substitute value of ${{y}_{1}}+{{y}_{2}}$ as 2k and ${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}$ as $4\left( {{k}^{2}}-4ah \right)$ in the equation (i) so we get,
$4\left( {{k}^{2}}-4ah \right)\left( 1+{{\left( \dfrac{2k}{4a} \right)}^{2}} \right)=4{{c}^{2}}$
Now on simplification we get,
$\left( {{k}^{2}}-4ah \right)\left( 1+\dfrac{{{k}^{2}}}{4{{a}^{2}}} \right)={{c}^{2}}$
Hence on cross multiplication we get,
$\left( {{k}^{2}}-4ah \right)\left( 4{{a}^{2}}+{{k}^{2}} \right)=4{{a}^{2}}{{c}^{2}}$
Now putting back has x and k as y so we get,
$\left( {{y}^{2}}-4ax \right)\left( {{y}^{2}}+4{{a}^{2}} \right)=4{{a}^{2}}{{c}^{2}}$
So, the correct option is (d).

Note: Student while forming the equation always compare the unknown value to the known values as we know the length of chords which was constant and compare it by the distance between variable $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ to form master equation.