Question

In a network shown, each resistance is equal to $R$. The equivalent resistance between adjacent corners A and D is:

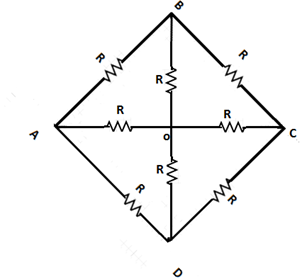
A. $R$
B. $\dfrac{2}{3}R$
C. $\dfrac{3}{7}R$
D. $\dfrac{8}{15}R$

Answer 1

First redraw the resistor network to identify the interfaces and connection properly. Then, find out the equivalent resistance of resistors connected in series and resistors connected in parallel at different interfaces. Then find the equivalent resistance of the network between the adjacent corners A and D.

Formula used:
$\text{Equivalent resistance of series combination, R =}{{\text{R}}_{1}}+{{R}_{2}}+{{R}_{3}}....+{{R}_{n-1}}+{{R}_{n}}=\sum\limits_{i=1}^{N}{{{R}_{i}}}$
$\text{Equivalent resistance of parallel combination,R=}{{\left( \dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}....+\dfrac{1}{{{R}_{n-1}}}+\dfrac{1}{{{R}_{n}}}=\dfrac{1}{\sum\limits_{i=1}^{N}{{{R}_{i}}}} \right)}^{-1}}$

Complete answer:
Let’s redraw the circuit.

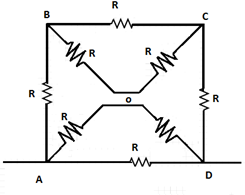
Now find the equivalent resistance across BC.
Here two resistors are connected in series and one resistor is connected in parallel. Two resistors in series have total resistance $=R+R=2R$.
Then, $Equivalent\text{ }resistance\text{ }across\text{ }BC={{\left[ \dfrac{1}{2R}+\dfrac{1}{R} \right]}^{-1}}=\dfrac{2R}{3}$

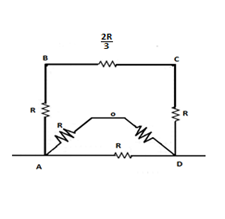
Now find resistance along ABCD.
Here all three resistors are connected in series. Then,
$Equivalent\text{ }resistance\text{ }along\text{ ABCD}=\dfrac{2R}{3}+R+R=\dfrac{8R}{3}$
Now find resistance across AD.
Here two series connected resistors of equivalent resistance $2R$, are connected in parallel with another two resistors of resistance $R$ and $\dfrac{8R}{3}$.

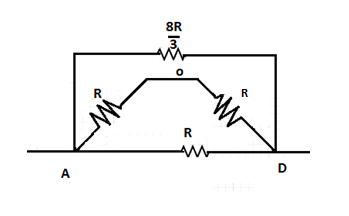
Then,
$Equivalent\text{ }resistance\text{ }across\text{ AD},{{R}_{AD}}={{\left[ \dfrac{3}{2R}+\dfrac{3}{8R} \right]}^{-1}}=\dfrac{16R}{30}=\dfrac{8R}{15}$
$Equivalent\text{ }resistance\text{ }acorss\text{ AD}=\dfrac{8R}{15}$

So, the correct answer is “Option D”.

Note:
Strategy to simplify a complicated circuit with resistors in series and parallel is, to begin from a point which is away from the component of interest. Then, replace all the series or parallel resistors with their equivalent resistor. Continue simplifying until a single equivalent resistor represents the entire resistor network.