Solveeit Logo
Login

Question

Question: In a metre bridge, the balancing length from the left end (standard resistance of one ohm is in the ...

In a metre bridge, the balancing length from the left end (standard resistance of one ohm is in the right gap) is found to be 20cm20{\rm{ cm}}. The value of the unknown resistance is
A. 4Ω4{\rm{ }}\Omega
B. 0.5Ω0.5{\rm{ }}\Omega
C. 0.4Ω0.4{\rm{ }}\Omega
D. 0.25Ω0.25{\rm{ }}\Omega

Explanation

Solution

The ratio of resistances on the left end and right end of the given meter bridge will be equal to the ratio of the distance between the left end and right end and jockey. We will use this expression for the metre bridge to calculate the value of unknown resistance.

Complete step by step answer:
Given:
The balancing length from the left end is l=20cml = 20{\rm{ cm}}.
The value of resistance in the right gap is R2=1Ω{R_2} = 1{\rm{ }}\Omega .

We have to find the value of unknown resistance R2{R_2}.

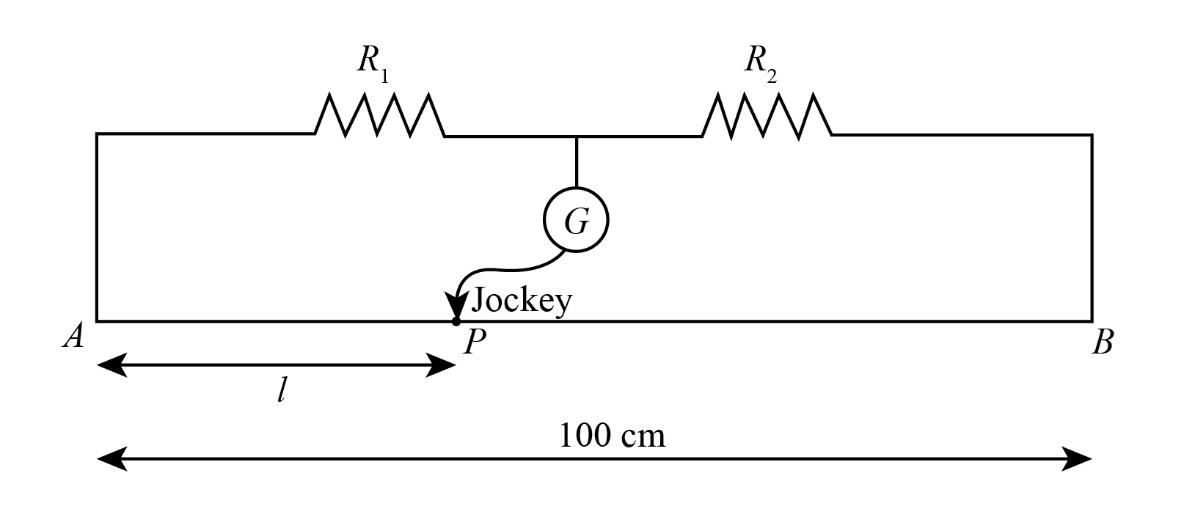
It is given that the metre bridge is in a balanced condition, so the value of the current through the jockey will be zero.

We can write the expression for balanced metre bridge as below:
R1R2=APBP\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{\rm{AP}}}}{{{\rm{BP}}}}……(1)

We know that the length of the metre bridge is 100cm100{\rm{ cm}}.
AB=100cm{\rm{AB}} = 100{\rm{ cm}}

Therefore from the above diagram, we can say that the distance between point B and point P is (100−l)cm\left( {100 - l} \right){\rm{ cm}}.
BP=(100cm−l){\rm{BP}} = \left( {100{\rm{ cm}} - l} \right)

Substitute ll for AP and (100cm−l)\left( {100{\rm{ cm}} - l} \right) for BP in equation (1).
R1R2=l(100cm−l)\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{l}{{\left( {100{\rm{ cm}} - l} \right)}}

Substitute 20cm20{\rm{ cm}} for l and 1Ω1{\rm{ }}\Omega for R2{R_2} in the above expression.

\dfrac{{{R_1}}}{{1{\rm{ }}\Omega }} = \dfrac{{20{\rm{ cm}}}}{{100{\rm{ cm}} - 20{\rm{ cm}}}}\\\ {R_1} = 0.25{\rm{ }}\Omega \end{array}$$ Therefore, the value of unknown resistance is $$0.25{\rm{ }}\Omega $$ **So, the correct answer is “Option D”.** **Note:** In metre bridge, a wire of length one-metre having uniform cross-sectional area is mounted between two clips of metals which are bent at right angles in such a way that the provision for the introduction of two resistors is provided. A battery is connected to the endpoints of the wire. Also, there is a galvanometer whose one end is connected to the strip and another to a jockey. This jockey is moved across the length of the wire, and unknown resistance is calculated.