Question

In a meter bridge, the wire of the length 1m has a non-uniform cross- section such that, the variation $\dfrac{dR}{dl}$ of its resistance R with length l is $\dfrac{dR}{dl}\propto \dfrac{1}{\sqrt{l}}$ . Two equal resistances are connected as shown in figure. The galvanometer has zero deflection when the jockey is at the point P. What the length AP is:

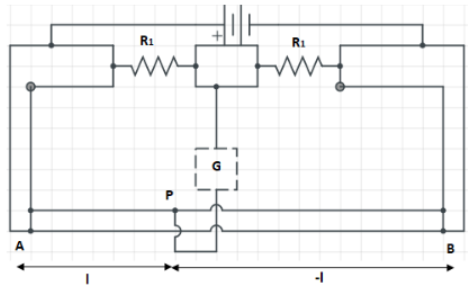
$\begin{aligned} & A.0.2m \\\ & B.0.3m \\\ & C.0.25m \\\ & D.0.35m \\\ \end{aligned}$

Answer 1

According to wheat stone’s bridge when the galvanometer shows zero deflection, we can use balanced condition. Therefore use balanced conditions. Then take resistances of point AD and DB as $R_1$ and $R_2$, since wire is not uniform. Apply expression, given in question. Replace R by $R_1$ and $R_2$, we get two equations. Integrate both the equation and equate it to get length of AD wire.

Complete answer:

Question stated that $\dfrac{dR}{dl}$ is varying like,
$\dfrac{dR}{dl}\propto \dfrac{1}{\sqrt{l}}$
Total length of wire AB is 1m which has non- uniform cross-section. Thus, for the given wire:
$dR=C\dfrac{dl}{\sqrt{l}}........(1)$
Where, C = constant
It is mentioned that the resistance attached is the same. Let $R_1$ be the resistance of part AD and $R_2$ be the resistance of part DB. According to balanced condition of wheat stone’s network,
$\begin{aligned} & \dfrac{{{R}^{'}}}{{{R}^{'}}}=\dfrac{{{R}_{1}}}{{{R}_{2}}} \\\ & \therefore {{R}_{1}}={{R}_{2}}......(2) \\\ \end{aligned}$
Now use equation (1)
Put $R =R_1$ in equation (1), we get
$d{{R}_{1}}=C\dfrac{dl}{\sqrt{l}}$
Integrate, we get
$\begin{aligned} & \int{d{{R}_{1}}}=C\int\limits_{0}^{l}{\dfrac{dl}{\sqrt{l}}} \\\ & \therefore {{R}_{1}}=C\int\limits_{0}^{l}{{{l}^{-\dfrac{1}{2}}}dl=C.2}\sqrt{l} \\\ \end{aligned}$
Similarly for $R=R_2$
Therefore, $\int{d{{R}_{2}}}=C\int\limits_{1}^{l}{{{l}^{-\dfrac{1}{2}}}dl=C\left( 2-2\sqrt{l} \right)}$
According to condition given in equation (2), we get,
$\begin{aligned} & C2\sqrt{l}=C\left( 2-2\sqrt{l} \right) \\\ & 2\sqrt{l}=2-2\sqrt{l} \\\ & 4\sqrt{l}=2 \\\ & 16l=4 \\\ & l=\dfrac{4}{16} \\\ & l=\dfrac{1}{4} \\\ & l=0.25m \\\ \end{aligned}$
Hence the length of AD is 0.25m.

Therefore option (C) is the correct option.

Note:
Meter Bridge is the modification of the wheat stone’s network. Wheatstone’s network is used to determine the value of the unknown resistance. Since the length of the wire used is one meter therefore it is called a meter Bridge. The balancing condition for Wheatstone’s network can also be determined by using ohm’s law.