Question
Question: In a meter bridge [Fig], the balance point is found to be at \[39.5\] cm from the end A, when the re...
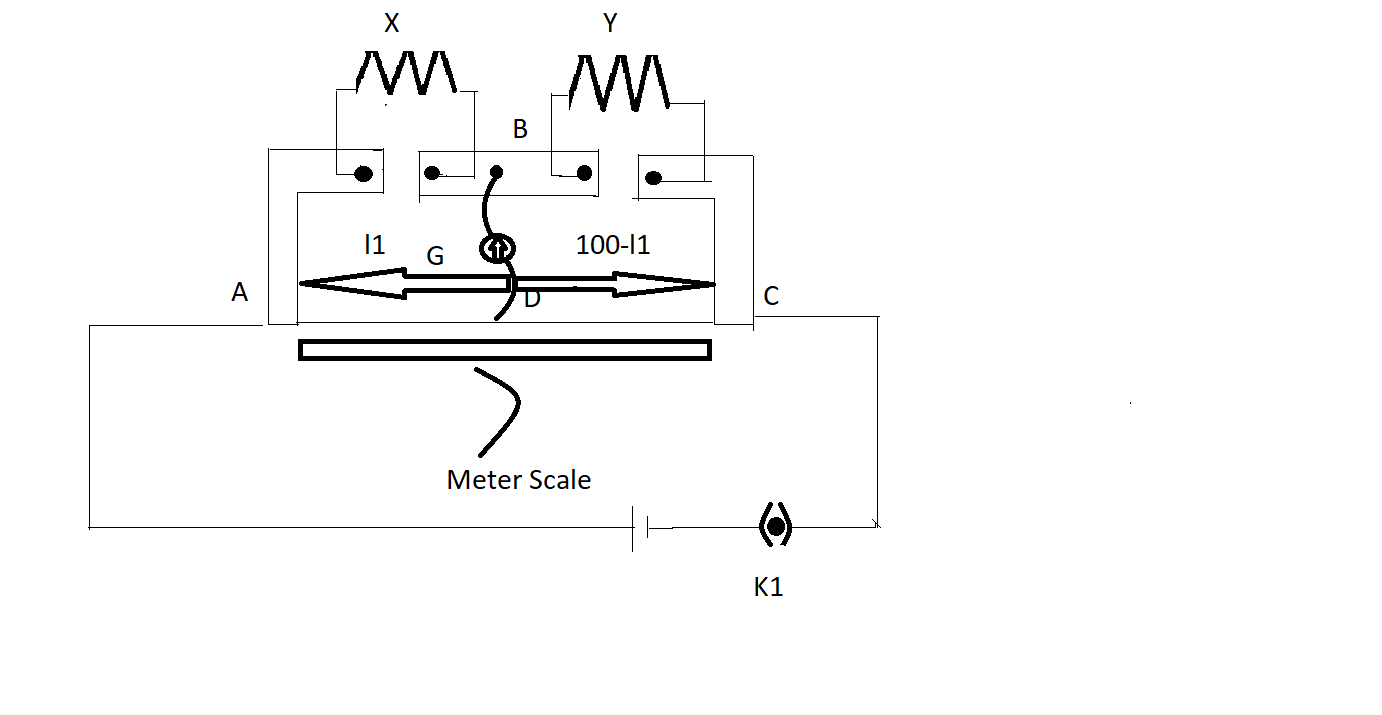
In a meter bridge [Fig], the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5 Ω. Determine the resistance of X . Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips? Determine the balance point of the bridge above if X and Y are interchanged. What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?
Solution
A meter bridge similarly called a slide wire interface is an instrument that works on the standard of a Wheatstone bridge. A meter bridge is used in tracking down the unknown resistance of a conductor as that of a Wheatstone bridge. We can find the resistance Y by using the condition for the balance of the meter bridge.
Complete step by step solution:
From the end A the balance point is given as 39.5 and also the resistance of Y is given as 12.5 Ω. To determine the resistance of X we need to use the condition of balance of the meter bridge
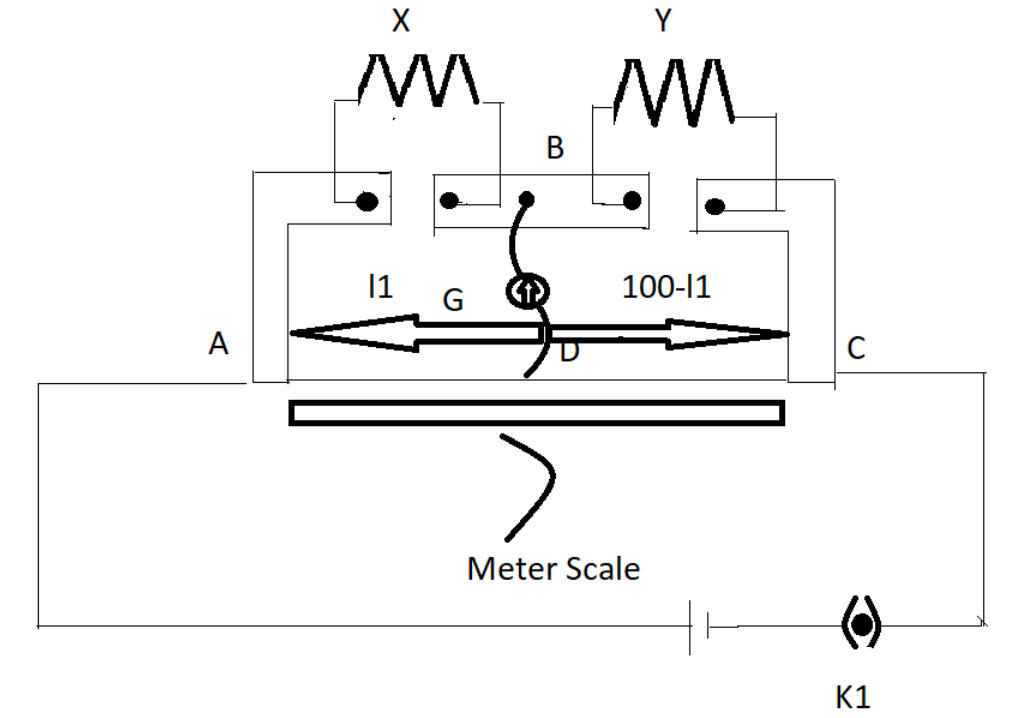
The condition of the balance of the meter bridge is given as
YX=l1(100−l1)
Here Y is the known resistance given asY=12.5 Ω
l1is the balance point from the end A. l1is given as39.5cm.
Now rearranging the above equation,
X=Yl1(100−l1)
Substituting the known values we get,
X=12.5×39.5(100−39.5)
When solving the above equation we get,
X=8.2Ω
There the resistance of X is X=8.2Ω
Also, connections between resistors in a Wheatstone or meter bridge are made of thick copper strips because the thick copper strips minimize the resistance so that we do not consider that resistance in the bridge formula.
B. The next question is to determine the balance point of the bridge above if X and Y are interchanged.
If we interchange the X and Y then the balance point l1 and 100−l1 will be interchanged.
The balance point from end A will be 100−l1.
Therefore we will get 100−l1=100−39.5=60.5cm.
Therefore, we will get the balance point as 60.5 cm from A.
C.What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?
Although the galvanometer and the cell are interchanged the balance point will not be changed. It will remain unchanged.
Hence the galvanometer will show no current.
Note:
In a wheat-stone bridge, we will have four resistance in total. In that, there will be two known resistances and two unknown resistances. From there, if we put the value of one resistance then we can find out what value of resistance we should put to make the bridge in a balanced condition.
