Question

In a meter-bridge experiment with resistance ${{R}_{1}}$​ in the left gap and resistance $X$ in the right gap, the null point is obtained at $40cm$ from the left end. With a resistance, ${{R}_{2}}$​ in the left gap, and the same resistance $X$ in the right gap, the null point is obtained at $50cm$ from the left end. Where will be the null point if ${{R}_{1}}$ and ${{R}_{2}}$​ are put first in series and then in parallel, in the left gap and right gap still containing $X$?

Answer 1

The length of the meter bridge wire is one metre. Analyze the cases explained in the equation using the equation of the meter bridge. Obtain the values of the resistances from the equations and apply them in the third case. These all may help you to solve this question.

Complete step-by-step solution:
The equation of the meter bridge is given by the Wheatstone principle,
$X=\dfrac{R\left( 100-L \right)}{L}$
Where $R$ be the known resistance, $X$ be the unknown resistance, $L$ be the balancing length.

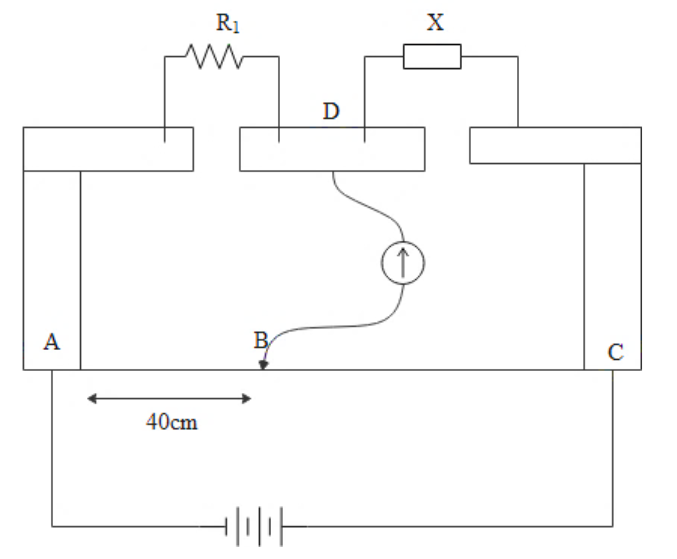
The first cases can be expressed as,
$\dfrac{{{R}_{1}}}{40}=\dfrac{X}{60}$
Simplifying the equation,
${{R}_{1}}=\dfrac{2}{3}X$
Where the balancing length is given as,
$L=40cm$
In the second case, we can write that,
As the balancing length is given as,
$L=50cm$

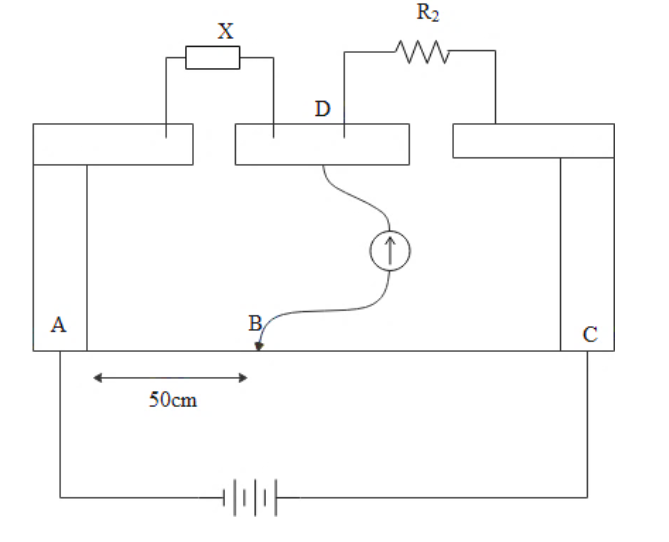
Substituting this in the equation,
$\dfrac{{{R}_{2}}}{50}=\dfrac{X}{50}$
Simplifying the equation,
${{R}_{2}}=X$
So now both the value of the resistances have been obtained.
So now let us take the condition where the resistance is in series connection,
$\dfrac{{{R}_{1}}+{{R}_{2}}}{{{y}_{1}}}=\dfrac{X}{100-{{y}_{1}}}$
Where ${{y}_{1}}$ be the null point in this condition,

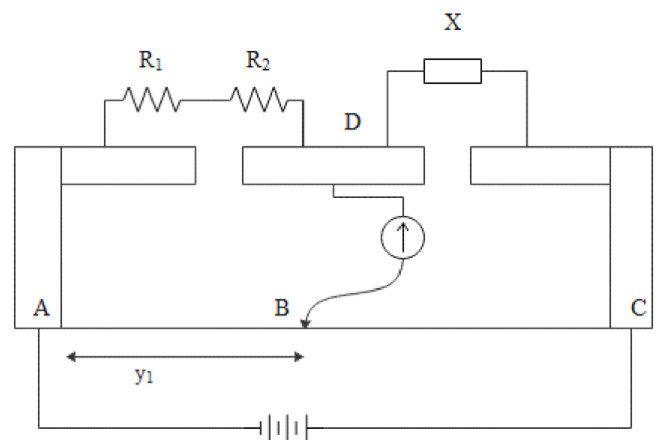
Substitute the values of resistances in the equation,

& \dfrac{\dfrac{2}{3}X+X}{{{y}_{1}}}=\dfrac{X}{100-{{y}_{1}}} \\\ & \dfrac{\dfrac{5}{3}X}{{{y}_{1}}}=\dfrac{X}{100-{{y}_{1}}} \\\ \end{aligned}$$ Simplifying and rearranging the equation will give, $$\begin{aligned} & \dfrac{5}{3{{y}_{1}}}= \dfrac{1}{100-{{y}_{1}}} \\\ &\Rightarrow 500-5{{y}_{1}}=3{{y}_{1}} \\\ &\Rightarrow 8{{y}_{1}}=500 \\\ \end{aligned}$$ From this, we will get the value of the null point in this condition. That is, $${{y}_{1}}=62.5cm$$ Let us consider the situation at which the resistance is connected in parallel. Let us assume that the balancing length is $${{y}_{2}}$$.  So applying the condition in the equation, $$\dfrac{\dfrac{{{R}_{1}}\times {{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}}{{{y}_{2}}}=\dfrac{X}{100-{{y}_{2}}}$$ Substitute the values in the equation will give, $$\dfrac{\dfrac{X\times \dfrac{2}{3}X}{X+\dfrac{2}{3}X}}{{{y}_{2}}}=\dfrac{X}{100-{{y}_{2}}}$$ Simplifying the equation will give, $$\dfrac{2}{5{{y}_{2}}}=\dfrac{1}{100-{{y}_{2}}}$$ $$\Rightarrow 200-2{{y}_{2}}=5{{y}_{2}}$$ From this equation, we will get the null point, $${{y}_{2}}=\dfrac{200}{7}=28.57cm$$ Therefore the answer for the question has been obtained. **Note:** The Wheatstone bridge is working on the basis of the principle of null deflection. This means that the ratio of the resistances will be equal and no current flows through the circuit. Under normal conditions, the bridge is in the unbalanced condition, therefore current will flow through the galvanometer.