Question
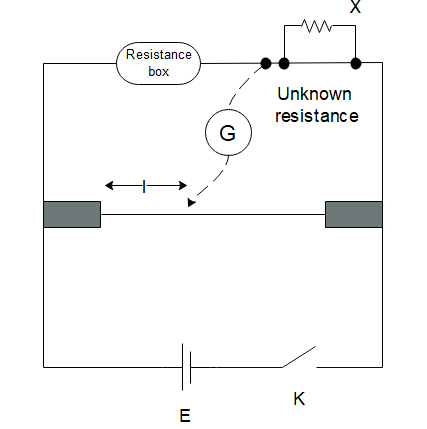
Question: In a meter bridge experiment, the circuit diagram, and the corresponding observation table are shown...
In a meter bridge experiment, the circuit diagram, and the corresponding observation table are shown in the figure.
| S.No. | R (Ω) | I(cm) |
|---|---|---|
| 1. | 1000 | 60 |
| 2. | 100 | 13 |
| 3. | 10 | 1.5 |
| 4. | 1 | 1.0 |
Which of the readings is inconsistent?
A) 4
B) 1
C) 2
D) 3
Solution
In this solution, we will use the formula of the balancing length of the meter bridge. The balancing length of the metre bridge depends on the value of the unknown and the known resistances in the circuit.
Formula used: In this solution, we will use the following formula
x=lR(100−l) where x is the value of the unknown resistance and l is the length of the bridge which is 1 metre or 100 cm and R is the value of the resistance box.
Complete step by step answer:
A meter bridge is an instrument that is used to find the value of unknown resistance. It works on the concepts of a Wheatstone bridge. The value of the unknown resistance is given by the formula x=lR(100−l).
The first column in the table given to us corresponds to the different values of unknown resistances whose value is determined from the metre bridge and their correspond balancing lengths are given in column 2.
So, using the formula for balancing lengths for
First case: x=401000×(100−60)≈667Ω
Second case: x=13100×(100−13)≈669Ω
Third case: x=1.510×(100−1.5)≈656Ω
Fourth case: x=11×(100−1)=99Ω
Hence, we can see that the value of the unknown resistance as determined from the fourth case is completely off from the rest of the three cases. Hence the 4th measurement is incorrect so option (A) is the correct choice.
Note: Since we want to find the value of the unknown resistance, the value determined of the unknown resistance for different known resistance boxes must be the same. Hence, we should not make the mistake of substituting the value of the resistances given in the table as the unknown resistance.
