Question
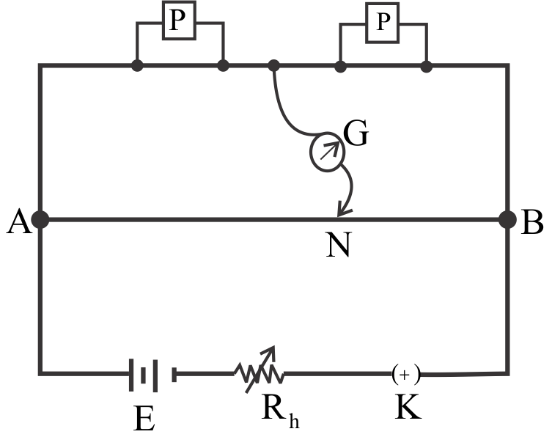
Question: In a meter bridge experiment resistances are connected as shown in figure. Initially resistance \(P ...
In a meter bridge experiment resistances are connected as shown in figure. Initially resistance P=4Ω and the neutral point N is at 60cm from A. Now an unknown resistance R is connected in series to P and the new position of the neutral point is at 80cm from A. The value of unknown resistance R is:
(A) 6Ω
(B) 7Ω
(C) 533Ω
(D) 320Ω
Solution
Using the formula of a meter bridge, first calculate the value of the resistance Q. Then with this value of Q we can determine the value of the unknown resistance R using the same formula.
Formula used
lX=100−lR, where X is the known resistance and Ris the unknown resistance and l is in cm.
Complete step by step solution
A meter bridge is an electrical instrument that works on the principle of a Wheatstone bridge. It is used in finding the unknown resistance of a conductor.
It consists of a long wire of 1m which is separated into two sections. In the left section we attach the known resistance and in the right section, we attach the unknown resistance. A jockey is present to detect the balance point. The galvanometer indicates the balance point. The balance point is the point on the wire where the galvanometer shows zero deflection.
Let X be the known resistance and R be the unknown resistance.
Then we can write,
lX=100−lR
Using this formula we can determine the value of the unknown resistance.
The distance between A and B is 100cm
It is given that AN=60cm
So, NB would be equal to (100−60)cm=40cm
From this diagram we can see that,
ANP=NBQ ⇒604=40Q ⇒Q=616 ⇒Q=38Ω
Now when another resistance R is connected in series with P, AN becomes 80cm
So, the value of the unknown resistance becomes,
80P+R=20Q ⇒44+R=38 ⇒12+3R=32 ⇒3R=20 ⇒R=320Ω
So, the value of the unknown resistance R is 320Ω
Therefore, the correct option is D.
Note: The main function of a meter bridge is to find the value of an unknown resistance. Another one of its functions is to compare two different resistances.
