Question

In a medium of refractive index 1.6 and having a convex surface has a point object in it at a distance of 12 cm from the pole. The radius of curvature is 6 cm. Locate the image as seen from air
A. A real image at 30 cm
B. A virtual image of 30 cm
C. A real image at 4.28 cm
D. A virtual image at 4.28 cm

Answer 1

Use the equation for refraction at a spherical interface of two mediums. i.e. $\dfrac{{{\mu }_{r}}}{v}-\dfrac{{{\mu }_{i}}}{u}=\dfrac{{{\mu }_{r}}-{{\mu }_{i}}}{R}$ and find the position of the image. If v is positive then the image is real and if v is negative then the image is virtual.

Formula used:
$\dfrac{{{\mu }_{r}}}{v}-\dfrac{{{\mu }_{i}}}{u}=\dfrac{{{\mu }_{r}}-{{\mu }_{i}}}{R}$
Here, v, u and R are the positions of the image, object and the radius of the spherical surface with respect to the pole and according to the sign convection. ${{\mu }_{i}}$ is the refractive of the medium from which the light rays are refracted and ${{\mu }_{r}}$ is the refractive of the medium in which the light rays enter after refraction.

Complete step by step answer:
To understand the given problem better, draw a figure for according to the given data.
It is given that it is a medium with refractive 1.6. It is said that it has a convex surface. An object is placed inside the medium at a distance of 12 cm from the pole (as shown in the figure below). The radius of curvature of the convex surface is given to 6cm.The other side of the medium is air.

To locate the image from the object when seen from the air, we use the equation for refraction at a spherical surface.
i.e. $\dfrac{{{\mu }_{r}}}{v}-\dfrac{{{\mu }_{i}}}{u}=\dfrac{{{\mu }_{r}}-{{\mu }_{i}}}{R}$ …. (i).
Here, v, u and R are the positions of the image, object and the radius of the spherical surface with respect to the pole and according to the sign convection. ${{\mu }_{i}}$ is the refractive of the medium from which the light rays are refracted and ${{\mu }_{r}}$ is the refractive of the medium in which the light rays enter after refraction.

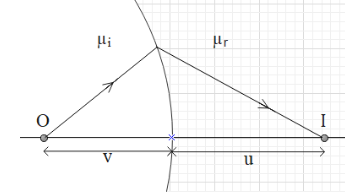
In this case, the light rays from the object are passing through the medium of refractive 1.6, initially and then enter into air and meet at a point where the image is formed. The refractive index of air is 1.
This means that ${{\mu }_{i}}=1.6$ and ${{\mu }_{r}}=1$.
According to the sign convection, $u=-12cm$ and $R=-6cm$.
Substitute the values in (i).
$\Rightarrow \dfrac{1}{v}-\dfrac{1.6}{-12}=\dfrac{1-1.6}{-6}$
$\Rightarrow \dfrac{1}{v}=\dfrac{0.6}{6}-\dfrac{1.6}{12}$
$\Rightarrow \dfrac{1}{v}=\dfrac{1.2}{12}-\dfrac{1.6}{12}\\\ \Rightarrow \dfrac{1}{v} =\dfrac{0.4}{12}\\\ \Rightarrow \dfrac{1}{v} =\dfrac{1}{30}$
$\therefore v=-30cm$.
This means that the image is formed at a distance of 30 cm from the pole. But since v is negative, it means that the image is formed in the medium where the object is placed.
This means that the image formed is virtual.

Therefore, the correct option is B.

Note: Some students may get confused because we know that a convex surface is meant to a converging surface. This means that the light rays converge at a point on the other side (in the other medium) and a real image is formed. However, it is so in this case.This is because for the above case to take place, the refractive index in which the object is placed must be less than the refractive index of the medium on the other side. If the converse happens then the convex surface does act as a converging surface.