Question

In a hostel, 60 % of the students read Hindi newspapers, 40 % read English newspapers and 20 % read Hindi and English newspapers. A student is selected at random. Find the probability that he reads neither Hindi nor English newspapers.

Answer 1

First, we mark students reading Hindi as H and students reading English as E. So, we have P (H) = 60 % while P (E) = 40 %. Then using $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ we will find the probability of the student who read any of the two papers. Then, at last, we use $P\left( {{\left( A\cup B \right)}^{'}} \right)=1-P\left( A\cup B \right)$ to find the probability of the student to read none of the newspapers.

Complete step by step answer:
We are given the probability of the student reading Hindi, English, or both newspapers. Let us mark the student who read the Hindi newspaper as H and mark the student who read the English newspaper as E. We are given that the probability of the number of students reading the Hindi newspaper is 60 %.
$\Rightarrow P\left( H \right)=60\%$
On Simplifying, we get,
$\Rightarrow P\left( H \right)=\dfrac{60}{100}$
$\Rightarrow P\left( H \right)=0.6$
Also, we have that the probability of the student reading English newspapers is 40 %.
$\Rightarrow P\left( E \right)=40\%$
$\Rightarrow P\left( E \right)=\dfrac{40}{100}$
On simplifying, we get,
$\Rightarrow P\left( E \right)=0.4$
The probability of the student who read both the papers is 20 %. We know that the intersection represents the section which is common to both the events. So, we get,
$P\left( E\cap H \right)=20\%$
$\Rightarrow P\left( E\cap H \right)=\dfrac{20}{100}$
$\Rightarrow P\left( E\cap H \right)=0.2$
Now, we need to find the probability of the number of students who read none of the two newspapers. So to do so, we first have to find the probability of those students who read the newspaper.
We know the union represents the collection of both the events. So, we have to find $P\left( E\cup H \right).$ We know that,
$P\left( E\cup H \right)=P\left( E \right)+P\left( H \right)-P\left( E\cap H \right)$
Putting the values as,
$P\left( H \right)=0.6,P\left( E \right)=0.4,P\left( E\cap H \right)=0.2$
We get,
$P\left( E\cup H \right)=0.6+0.4-0.2$
$\Rightarrow P\left( E\cup H \right)=0.8$
Now, the probability that the student reads neither Hindi nor English is given as,
$P\left( {{H}^{'}}\cap {{E}^{'}} \right)=1-\text{ Probability that they read a newspaper}$
$\Rightarrow P\left( {{H}^{'}}\cap {{E}^{'}} \right)=1-P\left( H\cup E \right)$
As, $P\left( H\cup E \right)=0.8$ so we get,
$P\left( {{H}^{'}}\cap {{E}^{'}} \right)=1-0.8$
$\Rightarrow P\left( {{H}^{'}}\cap {{E}^{'}} \right)=0.2$

Therefore, the required probability is 0.2 or $\dfrac{1}{5}.$

Note: We will do this in an alternate way. We are given the probability of a student who reads English newspapers as P (E) = 40 % and one who reads Hindi newspapers as P (H) = 60 %. Also, one who reads both is given as $P\left( E\cap H \right)=20\%,$ We will use Venn Diagram to find the probability of those who read none of the two newspapers.

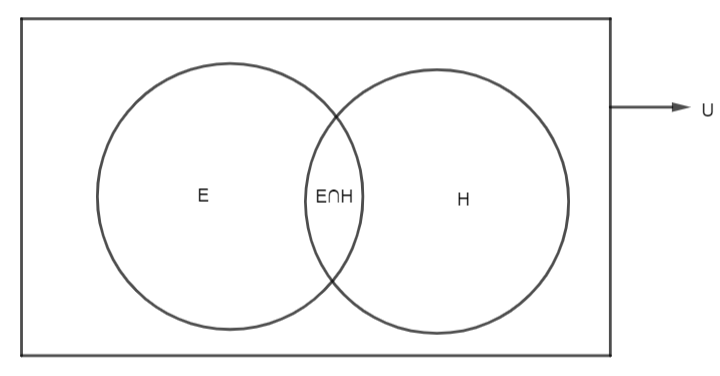
This shows the Venn diagram, the two circles tell us about the students who read Hindi or English newspapers. We have to find the probability that the student uses none of the two. So, the required probability is the shaded part.

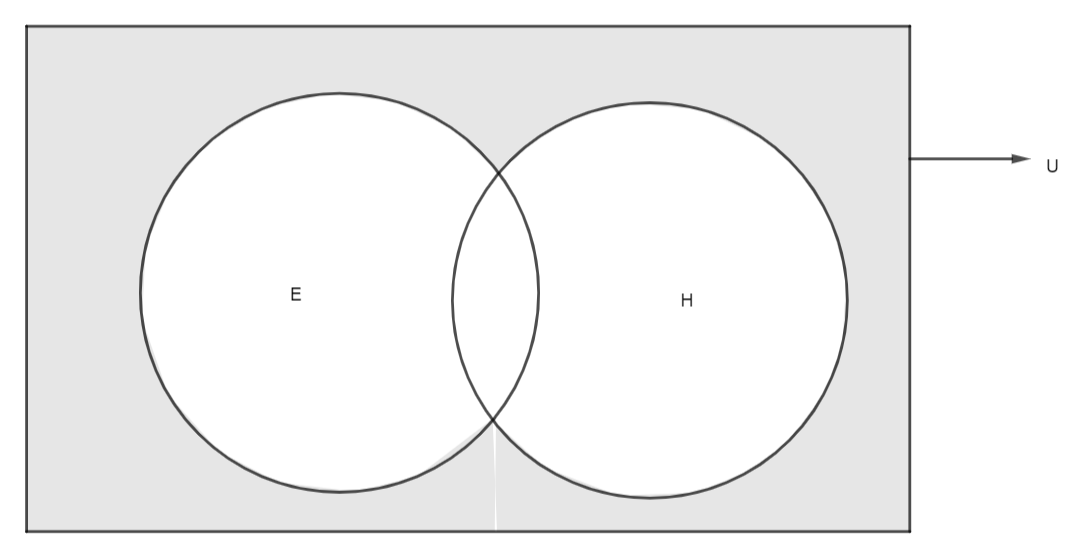
Clearly, to find this shaded part, we have to subtract $A\cup B$ from the total probability as the total probability is 1 always. So, the required probability will be $1-P\left( A\cup B \right).$
As we get,
$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$
So, we get,
$\Rightarrow P\left( A\cup B \right)=0.60+0.40-0.80$
Now using, $P\left( A\cup B \right)=0.80,$ we get the required probability of the student who reads none of the two newspaper as
$1-P\left( A\cup B \right)$
$\Rightarrow 1-0.8$
$\Rightarrow 0.20$
Hence, the required answer is 0.20.