Question

In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?

Answer 1

- Hint: In this question it is given that in a group of students,100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. We have to find how many students are there, so to understand it in better way we have to draw venn diagram,

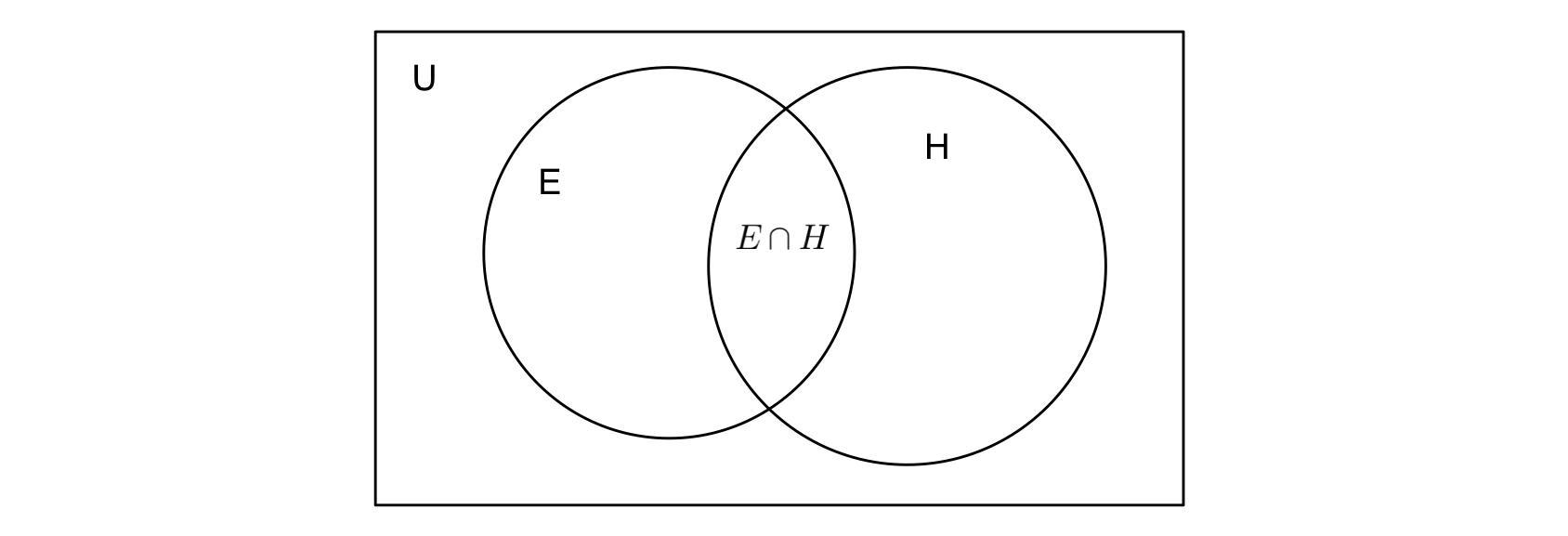
So to find the solution we need to know one formula which is, if A and B be two sets and if they have common elements then,
$n\left( A\cup B\right) =n\left( A\right) +n\left( B\right) -n\left( A\cap B\right)$.......(1)
Where n(A) is the number of elements in set A.

Complete step-by-step solution -
Let us consider
A= set of all students who know English.
H= set of all students who know Hindi.
Given the number of students who know Hindi is 100.
Therefore, $n\left( H\right) =100$
Also 50 students know English.
$n\left( E\right) =50$
25 students know English as well as Hindi,
$\therefore n\left( H\cap E\right) =25$
Now since the students either know English or Hindi.
So to find the total number of students we have to find the value of $n\left( H\cup E\right)$.
So by the formula (1) we can write,
$n\left( H\cup E\right) =n\left( H\right) +n\left( E\right) -n\left( H\cap E\right)$ [where A=H and B=E]
$\Rightarrow n\left( H\cup E\right) =100+50-25$
$\Rightarrow n\left( H\cup E\right) =150-25$
$\Rightarrow n\left( H\cup E\right) =125$
Hence, there are 125 students in the group.

Note: While solving this type of question you need to know that the union of two sets is a new set that contains all of the elements that are in at least one of the two sets. The union is written as $A\cup B$ or “A or B” and the intersection of two sets is a new set that contains all of the elements that are in both sets. The intersection is written as $A\cap B$ or “A and B”.