Question

In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French $= 17$, English $= 13$, Sanskrit $= 15$, French and English $= 09$, English and Sanskrit $= 4$, French and Sanskrit $= 5$, English, French and Sanskrit $= 3$. Find the number of students who study

1. Only Sanskrit
2. French and Sanskrit but not English

Answer 1

Here, we will find the number of students by using the concept of applications on the cardinality of the set. A set is defined as the collection of well defined objects. Cardinality of a set is defined as the number of elements in a set.

Complete step by step solution:
Let F be the number of students studying French, E be the number of students studying English, S be the number of students studying Sanskrit
Number of students studying French:
$n\left( F \right) = 17$
Number of students studying English:
$n\left( E \right) = 13$
Number of students studying Sanskrit:
$n\left( S \right) = 15$
Number of students studying French and English:
$n\left( {F \cap E} \right) = 09$
Number of students studying English and Sanskrit:
$n\left( {E \cap S} \right) = 4$
Number of students studying French and Sanskrit:
$n\left( {F \cap S} \right) = 5$
Number of students studying all the three languages:
$n\left( {F \cap E \cap S} \right) = 3$
Now, we have to find the number of students who study only Sanskrit.
Number of students who study only Sanskrit: $n\left( {\overline F \cap \overline E \cap S} \right) = n\left( S \right) - n\left( {F \cap S} \right) - n\left( {E \cap S} \right) + n\left( {F \cap E \cap S} \right)$
Substituting the values in the above equation, we get
$\Rightarrow n\left( {\overline F \cap \overline E \cap S} \right) = 15 - 5 - 4 + 3$
Adding and subtracting the terms, we get
$\Rightarrow n\left( {\overline F \cap \overline E \cap S} \right) = 9$
Now, we will find the number of students who study French and Sanskrit but not English.
$n\left( {F \cap \overline E \cap S} \right) = n\left( {F \cap S} \right) - n\left( {F \cap E \cap S} \right)$
Substituting the values in the above equation, we get
$\Rightarrow n\left( {F \cap \overline E \cap S} \right) = 5 - 3$
Subtracting the terms, we get
$\Rightarrow n\left( {F \cap \overline E \cap S} \right) = 2$

Therefore, the number of students who study only Sanskrit is $9$ and the number of students who study French and Sanskrit but not English is $2$.

Note:
We can also solve the problem on set by using venn diagrams. Venn diagram is a method to represent the relationships between the finite sets. A finite set is defined as the set which is countable.

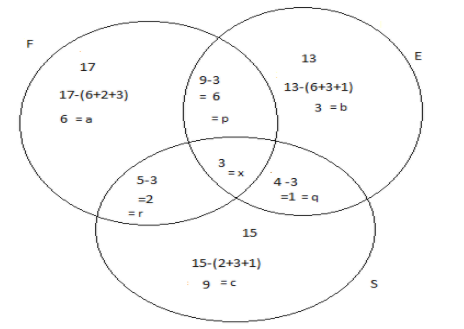
From the venn diagram, we get
Number of students who study only Sanskrit, $c = 9$
Number of students who study French and Sanskrit but not English, $r = 2$