Question

In a group of $200$ students, $20$ played cricket only, $36$ played tennis only, $40$ played hockey only, $8$ played cricket and tennis, $20$ played cricket and hockey, $28$ played hockey and tennis, and $80$ played hockey. By drawing a Venn diagram, find the number of students who
(i) Played cricket
(ii) Played tennis
(iii) Did not play any of the above three games.

Answer 1

For answering this question we will use the given information and draw the Venn diagram to represent the information assuming that the common part has $x$ students and Find the number of required numbers of students for the required cases.

Complete step-by-step solution
Now considering from the information given in the question we have a total of $200$ students, in which $20$ played cricket only, $36$ played tennis only, $40$ played hockey only, $8$ played cricket and tennis, $20$ played cricket and hockey, $28$ played hockey and tennis.
Let $x$ be the number of students who play all three games.
By using this information we can draw a Venn diagram representing this as shown below:

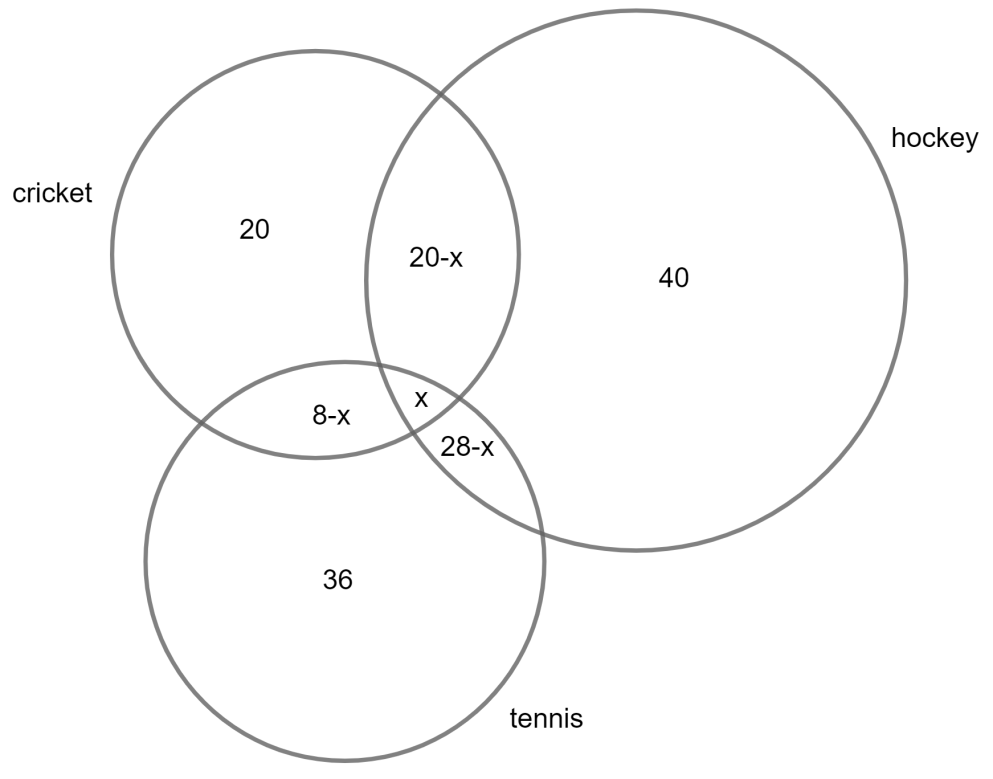
Here, each circle represents the number of students playing the game and the intersection part represents the common students playing both the games.
We have assumed the number of students playing all the 3 sports as $x$ on beforehand. The number of students playing any two games only will not include the number of students playing all the three games that are $x$. So we had subtracted $x$ in all three cases.
As it is given in the question that the total number of students playing hockey is $80$. Then the sum of all the parts of the circle will be equal to $80$ which is mathematically given as $40+20-x+x+28-x=80$.
By simplifying this we will have $x=8$.
Hence we can say that the total number of students playing cricket will be equal to the sum of all the parts of the circle which is mathematically given as $20+20-x+x+8-x=48-x=40$.
The number of students who played cricket is $40$.
Hence we can say that the total number of students playing tennis will be equal to the sum of all the parts of the circle which is mathematically given as $36+28-x+x+8-x=72-x=64$.
The number of students who played cricket is $64$.
The total number of students who did not play any of the above three games is the difference of the total number of students in the group from the total number of students who play at least one game which is mathematically given as $200-\left( 20+20-x+x+40+8-x+28-x+36 \right)=200-136=64$.
Hence we can conclude that the total number of students who did not play any of the above three games is $64$.

Note: While answering questions of this type we should be careful while drawing the Venn diagram and be sure with the calculations and we should make a note about the intersection part in every case because it is the repeated part. If we had made a mistake and written the number of students playing both cricket and tennis only that is $8-x$ as $10-x$ then we will have the total number of students playing cricket and tennis respectively as $20+20-x+x+10-x$ and $36+28-x+x+10-x$ after substituting the value of $x$ as $8$ we will have the number of students playing cricket and tennis are $42$ and $66$ respectively which is the wrong conclusion.