Question

In a group of 15 people, 7 read French, 8 read English while 3 of them read none of them. How many read French and English both?
$\begin{aligned} & \left( a \right)3 \\\ & \left( b \right)4 \\\ & \left( c \right)5 \\\ & \left( d \right)6 \\\ \end{aligned}$

Answer 1

Hint: To solve the question given above, we will make a venn diagram. First we will find out the actual number of people who read books. Then we will find out the number of people who are common to read both books with the help of venn diagrams.

Complete step-by-step answer:
In the question it is given that there are a total of 15 people. So, in the universal set we can say that there are 15 people. Thus n(U)=15 (Universal set is denoted by U). Now, we will assume that the total number of people who are reading at least one book is n (x) where x is the set of people who read at least one book. Now, it is given that 3 people do not read any book. They belong to set $\overline{x}$. Thus n($\overline{x}$)=3. Now, we know that the universal set will be the combination of set x and$\overline{x}$.
So $n\left( x \right)=n\left( 0 \right)-n\left( \overline{x} \right)\Rightarrow n\left( x \right)=15-3\Rightarrow n\left( x \right)=12$

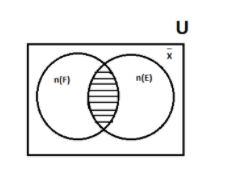
We can also say that the number of people who are reading French books are denoted by n (F). Thus n (F) =7. Similarly, we can say that n (E)=8. Now, we have to find the number of people who read both. This will be equal to the number of people in the set which is shown in the shaded portion. Now, we know that there are 12 actual readers. The total number of French readers=7 and the total number of English readers 8. Their total=8+7=15 readers. But the total actual readers are 12. So out of the 15 readers, some of them read both English and French and these are the extra readers that are denoted by the set in the shaded portion. So the extra readers will be =15-12=3 readers. Thus, these 3 read both English and French.
Hence option (a) is correct.

Note: The alternate method of solving the question is shown: we know that n (x)=12. We can also say that $x=F\bigcup E\Rightarrow N\left( x \right)=n\left( F\bigcup E \right).$ Now, we will apply the formula for $n\left( A\bigcup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\bigcap B \right).$
Thus, we have:
$\begin{aligned} & n\left( x \right)=n\left( F \right)+n\left( E \right)-n\left( F\bigcap E \right) \\\ & \Rightarrow 12=7+8-n\left( F\bigcap E \right) \\\ & \Rightarrow 12-15=-n\left( F\bigcap E \right) \\\ & \Rightarrow n\left( F\bigcap E \right)=3. \\\ \end{aligned}$
Where $\bigcap$ is the intersection symbol and denotes people who are common to both.