Question

In a golf tournament, if we designate the hole as the origin, and the putter (like a bat) is at $- 5.0\;m$ at time $0\;s$ , the velocity-time graph for the golf ball will be

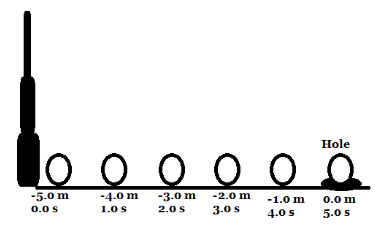
(A) a straight line inclined to the time axis
(B) a straight line parallel to the time axis
(C) a concave curve
(D) a convex curve

Answer 1

We will calculate the average velocity of the golf ball between every two consecutive positions given in the graph. We see that this value of the average velocity comes out to be $1\;m/s$ for every interval. So if we draw a velocity-time graph using this average velocity, it will turn out to be a straight line such that the velocity is $1\;m/s$ always irrespective of the time.

Complete Step by step solution:
From the question, it is clear that the golf ball is moving towards the hole from the putter as time increases.
We will calculate the velocity of the golf ball between every consecutive position and see the graph being formed.
Now, to calculate the velocity of the golf ball between positions $A$ and $B$ , we get ${v_{BA}} = \dfrac{{( - 4.0\;m) - ( - 5.0\;m)}}{{1.0\;s - 0.0\;s}}$ .
On simplifying, we get
${v_{BA}} = \dfrac{{1.0\;m}}{{1.0\;s}}$
Thus the velocity from position $A$ to position $B$ is ${v_{BA}} = 1\;m/s$ .
Similarly, we calculate the velocity of the golf ball between positions $B$ and $C$ and we get ${v_{CB}} = \dfrac{{( - 3.0\;m) - ( - 4.0\;m)}}{{2.0\;s - 1.0\;s}}$ .
On simplifying, we get
${v_{CB}} = \dfrac{{1.0\;m}}{{1.0\;s}}$
Thus the velocity from position $B$ to position $C$ is $1\;m/s$ .

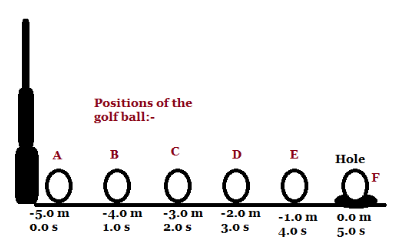
Similarly, we calculate the velocity of the golf ball between positions $C$ and $D$ and we get ${v_{DC}} = \dfrac{{( - 2.0\;m) - ( - 3.0\;m)}}{{3.0\;s - 2.0\;s}}$ .
On simplifying, we get
${v_{DC}} = \dfrac{{1.0\;m}}{{1.0\;s}}$
Thus the velocity from position $C$ to position $D$ is $1\;m/s$ .
Now we calculate the velocity of the golf ball between positions $D$ and $E$ , we get ${v_{ED}} = \dfrac{{( - 1.0\;m) - ( - 2.0\;m)}}{{4.0\;s - 3.0\;s}}$ .
On simplifying, we get
${v_{ED}} = \dfrac{{1.0\;m}}{{1.0\;s}}$
Thus the velocity from position $D$ to position $E$ is $1\;m/s$ .
On calculating the velocity of the golf ball between positions $E$ and $F$ , we get ${v_{FE}} = \dfrac{{(0.0\;m) - ( - 1.0\;m)}}{{5.0\;s - 4.0\;s}}$ .
On simplifying, we get
${v_{FE}} = \dfrac{{1.0\;m}}{{1.0\;s}}$
Thus the velocity from position $E$ to position $F$ is $1\;m/s$ .
We see that all the velocities turn out to be equal. The value of the velocities between every position is equal to $1\;m/s$ . Thus if we draw a graph of the velocity with respect to the time, we will get a straight line where the velocity will be uniform and invariable with respect to the time.
Thus the correct answer is option (B) a straight line parallel to the time axis.

Note: We can never say for sure whether the velocity of the ball will be absolutely uniform. This is because we have been supplied with discrete points. The average velocity between these points turns out to be uniform. However, the instantaneous velocities can vary a lot about which we have no information.