Solveeit Logo
Login

Question

Question: In a glass sphere, there is a small bubble \( 2 \times {10^{ - 2}}\,m \) from its centre. If the bub...

In a glass sphere, there is a small bubble 2×10−2 m2 \times {10^{ - 2}}\,m from its centre. If the bubble is viewed along the diameter of the sphere, from the side on which it lies, how far from the surface will it appear? The radius of glass sphere is 5×10−2 m5 \times {10^{ - 2}}\,m and refractive index of a glass is 1.5:1.5:
(A) 2.5×10−2 m2.5 \times {10^{ - 2}}\,m
(B) 3.2×10−2 m3.2 \times {10^{ - 2}}\,m
(C) 6.5×10−2 m6.5 \times {10^{ - 2}}\,m
(D) 0.2×10−2 m0.2 \times {10^{ - 2}}\,m

Explanation

Solution

We will apply the formula of the spherical refracting surface when the light rays comes from denser to rarer medium and then substitute the values of the refractive index, distance of the image and object and radius of curvature in it, to obtain the value.
We will use the formula for the spherical surfaces, that is,
(μ2v−μ1u)=μ2−μ1R\left( {\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u}} \right) = \dfrac{{{\mu _2} - {\mu _1}}}{R}
Where, μ2{\mu _2} = refractive index of the medium where the ray is going
μ1{\mu _1} = refractive index of the medium where the ray is coming
vv = distance of the image from the pole
uu = distance of the object from the pole
RR = radius of curvature

Complete step by step solution:
According to the question, we will draw a diagram that is given below:

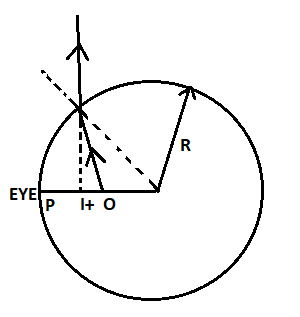
The values given in the question are as follows:
Refractive index of air is given by:
μ2=1{\mu _2} = 1
Refractive index of a glass is given by:
μ1=1.5{\mu _1} = 1.5
Distance of the object from the pole is given by:
u=5×10−2−3×10−2=2×10−2u = 5 \times {10^{ - 2}} - 3 \times {10^{ - 2}} = 2 \times {10^{ - 2}}
Radius of curvature is given by:
RR = 5×10−2 m5 \times {10^{ - 2}}\,m
Now using the formula of the refracting surface,
(μ2v−μ1u)=μ2−μ1R\left( {\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u}} \right) = \dfrac{{{\mu _2} - {\mu _1}}}{R}
Substituting the values, we get
(1v−1.53×10−2)=1−1.55×10−2\left( {\dfrac{1}{v} - \dfrac{{1.5}}{{3 \times {{10}^{ - 2}}}}} \right) = \dfrac{{1 - 1.5}}{{5 \times {{10}^{ - 2}}}}
After solving the equation, we get
v=2.5×10−2 mv = 2.5 \times {10^{ - 2}}\,m
Hence, the correct option is (A).

Note:
If the glass at one side is coated with the mercury surface, then the other side of the glass acts as the mirror by reflecting the light that enters it. But here the normal glass surface acts as the refracting surface by allowing the light through it. Hence the refracting formula is used.