Question

In a game of pool, the cue ball strikes another ball of the same mass and initially at rest. After the collision, the cue ball moves at $3.50\,m{s^{ - 1}}$ along a line making an angle of ${22.0^ \circ }$ with the cue ball’s original direction of motion, and the second ball has a speed of $2.00\,m{s^{ - 1}}$. Find
(a) the angle between the direction of motion of the second ball and the original direction of motion of the cue ball.
(b) the original speed of the cue ball.
(c) Is kinetic energy (of the centers of mass, don’t consider the rotation) conserved?

Answer 1

In this question, we use the concept of resolution of vectors along the axes and also the concept of conservation of the kinetic energy of a system which is when the change in kinetic energy of the system is zero, the kinetic energy is conserved.

Complete step by step answer:
Let us assume some terminologies of the given data for better understanding.

${v_i}$ - initial velocity of the cue ball before collision
${v_f}$ - final velocity of the cue ball after collision
${v_2}$ - velocity of the second ball
${\theta _1}$ - angle between original direction of cue ball and 1st deflected cue ball
${\theta _2}$ - angle between original direction of cue ball and 2nd deflected cue ball

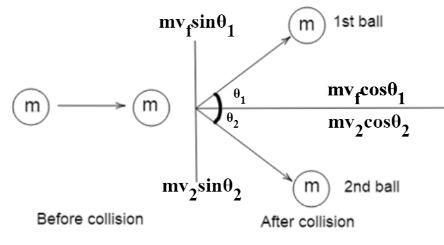
(a) Now, writing the given data, we have
${v_f} = 3.50m{s^{ - 1}}$ , ${\theta _1} = {22^ \circ }$ and ${v_2} = 2m{s^{ - 1}}$
Resolving along X-axis for conserving momentum,
$m{v_i} = m{v_f}\cos {\theta _1} + m{v_2}\cos {\theta _2} - - - - - - - - (1)$
Also, resolving along Y-axis, we get
$0 = - \sin {\theta _1} + m{v_2}\sin {\theta _2} - - - - - - - - (2)$
On solving, $\sin {\theta _2} = \dfrac{{{v_f}}}{{{v_2}}}\sin {\theta _1}$
$\sin {\theta _2} = \dfrac{{3.5}}{2}\sin ({22^ \circ })$
$\Rightarrow {\theta _2} = {\sin ^{ - 1}}(0.655)$
$\therefore {\theta _2} = {40^ \circ }57'$
Thus, the angle between the direction of motion of the second ball and the original direction of motion of the cue ball is ${\theta _2} = {40^ \circ }57'$.

(b) Using the eq $(1)$ for the momentum,
${v_i} = 3.5\cos ({22^ \circ }) + 2\cos ({40^ \circ }57')$
$\therefore {v_i} = 4.75\,m{s^{ - 1}}$
Hence, the original speed of the cue ball is $4.75m{s^{ - 1}}$ .

(c) Now, The change in kinetic energy of the system is given by
$\Delta K = {K_f} - {K_i}$
$\Rightarrow \Delta K = \dfrac{1}{2}m[v_f^2 + v_2^2 - v_i^2]$
Putting the values, we get
$\Rightarrow \Delta K = \dfrac{1}{2}m[{\left( {2.5} \right)^2} + {\left( 2 \right)^2} - {\left( {4.75} \right)^2}]$
$\therefore \Delta K = - 0.65\,kgm{s^{ - 1}}$
Thus, It is not zero and hence the kinetic energy is not conserved.

Note: When the two objects collide each other elastically and if their linear momentum kinetic energy remains conserved before and after collision, then the collision is called elastic collision, otherwise, it is called inelastic collision. Also, when two objects of equal mass collide elastically head on condition, they exchange their velocities. Some kinetic energy is always lost in an inelastic collision.